CF集萃2

最新推荐文章于 2019-06-24 11:02:04 发布

转载最新推荐文章于 2019-06-24 11:02:04 发布 · 106 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/huyufeifei/p/10761436.html

CF1155D - Beautiful Array

题意：给你一个序列和x，你可以选择任意一个子串(可以为空)乘上x，使得得到的序列最大子串和最大。求这个最大值。30w，2s。

解：设f_i,0/1/2表示序列前i个数还没乘x/正在乘x/乘完了x的最大后缀和。答案就是这个DP数组的最大值。

 1 #include <bits/stdc++.h>
 2 
 3 typedef long long LL;
 4 const int N = 300010;
 5 
 6 LL a[N], x, f[N][3];
 7 int n;
 8 
 9 int main() {
10     scanf("%d%lld", &n, &x);
11     for(int i = 1; i <= n; i++) {
12         scanf("%lld", &a[i]);
13     }
14     LL ans = 0;
15     for(int i = 1; i <= n; i++) {
16         f[i][0] = std::max(a[i], f[i - 1][0] + a[i]);
17         f[i][1] = std::max(std::max(a[i] * x, f[i - 1][1] + a[i] * x), f[i - 1][0] + a[i] * x);
18         f[i][2] = std::max(a[i], std::max(f[i - 1][2] + a[i], f[i - 1][1] + a[i]));
19         ans = std::max(std::max(ans, f[i][0]), std::max(f[i][1], f[i][2]));
20     }
21     printf("%lld\n", ans);
22     return 0;
23 }

AC代码

本题还有一种线段树做法。从左往右扫一遍，在每个位置考虑乘x的那一段的右端点在当前位置时的最大值。

那么右边要加上一个最大前缀。左边要在线段树上每个位置，维护以当前位置为乘x左端时的最大值。就是最大后缀 + (x - 1)a[i]

然后求个最大值就行了。

CF1117C - Magic Ship

题意：你要从(x1,y1)到(x2,y2)，你每天会走一格，还会被风吹一格。风向有个长为n的循环节。求最少要几天到达。n <= 1e5，坐标<=1e9。

解：发现某一天到达之后，接下来所有天都有办法到达。于是二分。

 1 #include <bits/stdc++.h>
 2 
 3 typedef long long LL;
 4 const int N = 100010;
 5 
 6 int x1, x2, Y1, Y2, n;
 7 char str[N];
 8 int dx[N], dy[N];
 9 
10 template <typename T> inline T abs(T x) {
11     return x < 0 ? -x : x;
12 }
13 
14 inline bool check(LL k) {
15     LL x = x1 + (k / n) * dx[n] + dx[k % n];
16     LL y = Y1 + (k / n) * dy[n] + dy[k % n];
17     return abs(x - x2) + abs(y - Y2) <= k;
18 }
19 
20 int main() {
21     scanf("%d%d%d%d", &x1, &Y1, &x2, &Y2);
22 
23     scanf("%d", &n);
24     scanf("%s", str + 1);
25 
26     for(int i = 1; i <= n; i++) {
27         dx[i] = dx[i - 1];
28         dy[i] = dy[i - 1];
29         if(str[i] == 'U') {
30             dy[i]++;
31         }
32         if(str[i] == 'D') {
33             dy[i]--;
34         }
35         if(str[i] == 'L') {
36             dx[i]--;
37         }
38         if(str[i] == 'R') {
39             dx[i]++;
40         }
41     }
42 
43     LL l = 0, r = 1e18;
44     while(l < r) {
45         LL mid = (l + r) >> 1;
46         if(check(mid)) {
47             r = mid;
48         }
49         else {
50             l = mid + 1;
51         }
52     }
53 
54     if(r == 1e18) r = -1;
55     printf("%lld\n", r);
56     return 0;
57 }

AC代码

CF1117D - Magic Gems

题意：你有很多个魔法宝石，每个可以变成m个普通宝石。你需要选出若干个魔法宝石，然后再选出若干个把它们变成普通宝石，以此来填满n个空格。问方案数。n <= 1e18，m <= 100。

解：枚举选多少个魔法宝石，发现答案其实就是这个东西：

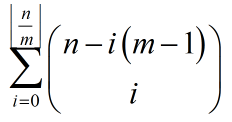
打表后发现f_n = f_n-1 + f_n-m。然而我们还有一种更优秀的推法：考虑最后一个空位是普通宝石还是魔法宝石即可。矩阵快速幂即可。

 1 #include <bits/stdc++.h>
 2 
 3 typedef long long LL;
 4 const int N = 110, MO = 1e9 + 7;
 5 
 6 int a[N][N], c[N][N], m, ans[N][N];
 7 LL n;
 8 
 9 inline void out(int (*a)[N]) {
10 
11     for(int i = 1; i <= m; i++) {
12         for(int j = 1; j <= m; j++) {
13             printf("%d ", a[i][j]);
14         }
15         puts("");
16     }
17     puts("");
18 
19     return;
20 }
21 
22 inline void mul() {
23     memset(c, 0, sizeof(c));
24     for(int k = 1; k <= m; k++) {
25         for(int i = 1; i <= m; i++) {
26             if(!ans[i][k]) {
27                 continue;
28             }
29             for(int j = 1; j <= m; j++) {
30                 c[i][j] = (c[i][j] + 1ll * ans[i][k] * a[k][j] % MO) % MO;
31             }
32         }
33     }
34     memcpy(ans, c, sizeof(ans));
35     return;
36 }
37 
38 inline void mulself() {
39     memset(c, 0, sizeof(c));
40     for(int k = 1; k <= m; k++) {
41         for(int i = 1; i <= m; i++) {
42             if(!a[i][k]) continue;
43             for(int j = 1; j <= m; j++) {
44                 c[i][j] = (c[i][j] + 1ll * a[i][k] * a[k][j] % MO) % MO;
45             }
46         }
47     }
48     memcpy(a, c, sizeof(c));
49     return;
50 }
51 
52 int main() {
53     scanf("%lld%d", &n, &m);
54 
55     if(n < m) {
56         printf("1");
57         return 0;
58     }
59 
60     for(int i = 1; i < m; i++) {
61         a[i + 1][i] = 1;
62     }
63     a[1][m] = a[m][m] = 1;
64     for(int i = 1; i <= m; i++) ans[i][i] = 1;
65 
66     LL t = n - m;
67     //out(a);
68     //out(ans);
69     while(t) {
70         if(t & 1) {
71             mul();
72             //out(ans);
73         }
74         mulself();
75         //out(a);
76         t = t >> 1;
77     }
78 
79     int res = 0;
80     for(int i = 1; i <= m; i++) {
81         res = (res + ans[i][m]) % MO;
82     }
83     res = (res + ans[m][m]) % MO;
84 
85     printf("%d\n", res);
86     return 0;
87 }

AC代码

CF1117E - Decypher the String

题意：存在一个长为n的字符串和n个swap操作，但是你都不知道。你只知道操作的结果。你可以询问三次，每次给定一个字符串，回答该字符串操作的结果。输出原串。n <= 10000。

解：可用的字符有26个。假如每次把集合s位置的字符变成a，那么操作后所有a的位置集合t和s之间就有一个双射。这样一次就可以把n / 26。发现26³ = 17576，刚好。

实现上就是用一个结构体表示一组双射，两个vector存s和t。每次把这个vector分段染色，然后输出，操作完之后进行分组。

  1 #include <bits/stdc++.h>
  2 
  3 const int N = 10010;
  4 /// 26 * 26 = 676
  5 struct Node {
  6     std::vector<int> a, b;
  7 }stk[N]; int top;
  8 
  9 char str[N], my[N];
 10 int n;
 11 
 12 inline void solve(const Node &x) {
 13     int lm;
 14     if(x.a.size() <= 26) {
 15         lm = 1;
 16     }
 17     else if(x.a.size() <= 676) {
 18         lm = 26;
 19     }
 20     else {
 21         lm = 676;
 22     }
 23     int p = 0;
 24     char c = 'a';
 25     for(int i = 0; i < (int)x.a.size(); i++) {
 26         my[x.a[i]] = c;
 27         ++p;
 28         if(p == lm) {
 29             p = 0;
 30             ++c;
 31         }
 32     }
 33     return;
 34 }
 35 
 36 inline void work(int i) {
 37     int lm;
 38     if(stk[i].a.size() <= 26) {
 39         lm = 1;
 40     }
 41     else if(stk[i].a.size() <= 676) {
 42         lm = 26;
 43     }
 44     else {
 45         lm = 676;
 46     }
 47     int p = 0, cnt = 1, f;
 48     for(int j = 0; j < (int)stk[i].a.size(); j++) {
 49         stk[top + cnt].a.push_back(stk[i].a[j]);
 50         ++p;
 51         f = cnt;
 52         if(p == lm) {
 53             p = 0;
 54             ++cnt;
 55         }
 56     }
 57 
 58     for(int j = 0; j < (int)stk[i].a.size(); j++) {
 59         int x = stk[i].b[j];
 60         stk[top + 1 - 'a' + my[x]].b.push_back(x);
 61     }
 62     stk[i] = stk[top + f];
 63     stk[top + f].a.clear(); /// !!! important
 64     stk[top + f].b.clear(); ///
 65     top = top + f - 1;
 66     return;
 67 }
 68 
 69 int main() {
 70     scanf("%s", str + 1);
 71     n = strlen(str + 1);
 72 
 73     top = 1;
 74     for(int i = 1; i <= n; i++) {
 75         stk[1].a.push_back(i);
 76         stk[1].b.push_back(i);
 77         my[i] = 'a';
 78     }
 79 
 80     for(int t = 1; t <= 3; t++) {
 81         //printf("t = %d \n", t);
 82         for(int i = 1; i <= top; i++) {
 83             //printf("i = %d \n", i);
 84             if(stk[i].a.size() > 1) {
 85                 solve(stk[i]);
 86             }
 87         }
 88         printf("? ");
 89         for(int i = 1; i <= n; i++) {
 90             putchar(my[i]);
 91         }
 92         puts("");
 93         fflush(stdout);
 94         scanf("%s", my + 1);
 95         int temp = top;
 96         for(int i = 1; i <= temp; i++) {
 97             if(stk[i].a.size() > 1) {
 98                 work(i);
 99             }
100         }
101     }
102 
103     for(int i = 1; i <= n; i++) {
104         my[stk[i].a[0]] = str[stk[i].b[0]];
105     }
106     printf("! ");
107     for(int i = 1; i <= n; i++) {
108         putchar(my[i]);
109     }
110     puts("");
111     return 0;
112 }

AC代码

这题还有一种CRT解法......

具体来说，对每个位置i，考虑它是从哪来的，设从pos来。

那么我们先询问三次，如下图。

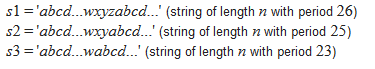
然后那么对于i来说，pos % 23 = s1[i] - 'a'。然后解方程即可。

CF1146G Zoning Restrictions

题意：你要在长为n的位置上填上[0, h]的数，如果填了x就会得到x²块钱。有m个限制，形如如果在[l, r]中有数超过了y，就要付c块钱。求最多钱数。n,m,h <= 50。

解：有一种网络流做法是最小割。

考虑切糕，把每个位置的取值都串起来，因为要最小，就先假设填了h，填x就是h² - x²。对于限制，额外连向一个新点，向t连边为c。

  1 #include <bits/stdc++.h>
  2 
  3 const int N = 100010, INF = 0x3f3f3f3f;
  4 
  5 struct Edge {
  6     int nex, v, c;
  7     Edge(){}
  8     Edge(int N, int V, int C) {
  9         nex = N;
 10         v = V;
 11         c = C;
 12     }
 13 }edge[1000010]; int tp = 1;
 14 
 15 int e[N], n, h, m, vis[N], d[N];
 16 std::queue<int> Q;
 17 
 18 inline void add(int x, int y, int z) {
 19     edge[++tp] = Edge(e[x], y, z);
 20     e[x] = tp;
 21     edge[++tp] = Edge(e[y], x, 0);
 22     e[y] = tp;
 23     return;
 24 }
 25 
 26 inline bool BFS(int s, int t) {
 27     static int Time = 0;
 28     Q.push(s);
 29     ++Time;
 30     vis[s] = Time;
 31     d[s] = 0;
 32     while(Q.size()) {
 33         int x = Q.front();
 34         Q.pop();
 35         for(int i = e[x]; i; i = edge[i].nex) {
 36             int y = edge[i].v;
 37             if(vis[y] != Time && edge[i].c) {
 38                 vis[y] = Time;
 39                 d[y] = d[x] + 1;
 40                 Q.push(y);
 41             }
 42         }
 43     }
 44     return vis[t] == Time;
 45 }
 46 
 47 int DFS(int x, int t, int maxF) {
 48     if(x == t) {
 49         return maxF;
 50     }
 51     int ans = 0;
 52     for(int i = e[x]; i; i = edge[i].nex) {
 53         int y = edge[i].v;
 54         if(d[x] + 1 != d[y] || !edge[i].c) {
 55             continue;
 56         }
 57         int temp = DFS(y, t, std::min(maxF - ans, edge[i].c));
 58         if(!temp) {
 59             d[y] = INF;
 60         }
 61         ans += temp;
 62         edge[i].c -= temp;
 63         edge[i ^ 1].c += temp;
 64         if(ans == maxF) {
 65             break;
 66         }
 67     }
 68     return ans;
 69 }
 70 
 71 inline int solve(int s, int t) {
 72     int ans = 0;
 73     while(BFS(s, t)) {
 74         ans += DFS(s, t, INF);
 75     }
 76     return ans;
 77 }
 78 
 79 inline int id(int x, int y) {
 80     return (x - 1) * (h + 2) + y + 1;
 81 }
 82 
 83 int main() {
 84     
 85     scanf("%d%d%d", &n, &h, &m);
 86     int s = (h + 2) * n + m + 1, t = s + 1, lm = (h + 2) * n, V = h * h;
 87     for(int i = 1; i <= n; i++) {
 88         add(s, id(i, 0), INF);
 89         add(id(i, h + 1), t, INF);
 90         for(int j = 0; j <= h; j++) {
 91             add(id(i, j), id(i, j + 1), V - j * j);
 92         }
 93     }
 94     for(int i = 1; i <= m; i++) {
 95         int l, r, x, y;
 96         scanf("%d%d%d%d", &l, &r, &x, &y);
 97         if(x == h) continue;
 98         int p = lm + i;
 99         add(p, t, y);
100         for(int j = l; j <= r; j++) {
101             add(id(j, x + 1), p, INF);
102         }
103     }
104     
105     int ans = n * h * h;
106     ans -= solve(s, t);
107     printf("%d\n", ans);
108     return 0;
109 }

AC代码

还有一种区间DP解法，我并不会...

CF1147D - Palindrome XOR

题意：求有多少对长度不超过n的无前导0的回文01串满足异或起来恰好为s。s的第一位一定是1，存在通配符。n <= 1000

解：这个1000很有趣....可以O(n)枚举第二个串的开头在哪。

然后发现这个回文和异或都是些形如“它们相等”或者“它们不等”的限制。于是考虑用并查集处理这些限制，每个连通块有两种取值。边带权并查集即可。

  1 #include <bits/stdc++.h>
  2 
  3 const int N = 1010, MO = 998244353;
  4 
  5 char str[N];
  6 int n;
  7 
  8 inline int qpow(int a, int b) {
  9     int ans = 1;
 10     while(b) {
 11         if(b & 1) ans = 1ll * ans * a % MO;
 12         a = 1ll * a * a % MO;
 13         b = b >> 1;
 14     }
 15     return ans;
 16 }
 17 
 18 namespace ufs {
 19     int cnt, fa[N * 2], val[N * 2];
 20     inline void init() {
 21         for(int i = 1; i <= n * 2 + 1; i++) {
 22             fa[i] = i;
 23             val[i] = 0;
 24         }
 25         cnt = 2 * n;
 26         return;
 27     }
 28     int find(int x, int &v) {
 29         if(x == fa[x]) {
 30             v = 0;
 31             return x;
 32         }
 33         int t = find(fa[x], v);
 34         v ^= val[x];
 35         fa[x] = t;
 36         val[x] = v;
 37         return t;
 38     }
 39     inline bool merge(int x, int y, int v) {
 40         int t, t2;
 41         x = find(x, t);
 42         y = find(y, t2);
 43         t ^= t2;
 44         if(x == y) {
 45             if(t != v) return false;
 46             return true;
 47         }
 48         else {
 49             fa[x] = y;
 50             val[x] = v ^ t;
 51             cnt--;
 52         }
 53         return true;
 54     }
 55 }
 56 using ufs::merge;
 57 
 58 int main() {
 59     scanf("%s", str + 1);
 60     n = strlen(str + 1);
 61     std::reverse(str + 1, str + n + 1);
 62     int ans = 0, Z = 2 * n + 1;
 63     for(int i = n - 1; i >= 1; i--) {
 64         ufs::init();
 65         if(!merge(n, Z, 1)) continue;
 66         if(!merge(1, Z, 1)) continue;
 67         if(!merge(n + 1, Z, 1)) continue;
 68         if(!merge(n + i, Z, 1)) continue;
 69         int fd = 0;
 70         for(int j = n; j > i; j--) {
 71             if(!merge(n + j, Z, 0)) {
 72                 fd = 1; break;
 73             }
 74         }
 75         if(fd) continue;
 76         for(int j = 1; j * 2 <= n; j++) {
 77             if(!merge(j, n - j + 1, 0)) {
 78                 fd = 1;
 79                 break;
 80             }
 81         }
 82         if(fd) continue;
 83         for(int j = 1; j * 2 <= i; j++) {
 84             if(!merge(n + j, n + i - j + 1, 0)) {
 85                 fd = 1;
 86                 break;
 87             }
 88         }
 89         if(fd) continue;
 90         for(int j = 1; j <= n; j++) {
 91             if(str[j] != '?') {
 92                 if(!merge(j, n + j, str[j] - '0')) {
 93                     fd = 1;
 94                     break;
 95                 }
 96             }
 97         }
 98         if(fd) continue;
 99         ans = (ans + qpow(2, ufs::cnt)) % MO;
100     }
101     printf("%d\n", ans);
102     return 0;
103 }

AC代码

转载于:https://www.cnblogs.com/huyufeifei/p/10761436.html