斐波那契额数列及青蛙跳台阶问题

题目：写一个函数，输入n，求斐波那契（Fibonacci）数列的第n项。

 斐波那契（Fibonacci）数列定义如下：

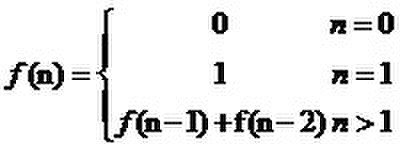
效率很低的解法：

1 2 3 4 5 6 7 8 9 10

long  long  Fibonacci_Solution1(unsigned  int  n) {      if (n <= 0)          return  0;        if (n == 1)          return  1;        return  Fibonacci_Solution1(n - 1) + Fibonacci_Solution1(n - 2); }

 

改进的算法：从下往上计算。首先根据f(0)和f(1)算出f(2)，再根据f(1)和f(2)算出f(3)。。。。。依此类推就可以算出第n项了。很容易理解，这种思路的时间复杂度是o(n)。实现代码如下：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

long  long  Fibonacci(unsigned n) {      int  result[2] = {0 , 1};      if (n < 2)          return  result[n];        long  long  fibMinusOne = 1;      long  long  fibMinusTwo = 0;      for (unsigned  int  i = 2 ; i <= n ; ++i)      {          fibN = fibMinusOne + fibMinusTwo;            fibMinusTwo = fibMinusOne;          fibMinusOne = fibN;      }            return  fibN; }

 

题目：一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

 

可以把n级台阶时的跳法看成是n的函数，记为f(n)。当n>2时，第一次跳的时候就有两种不同的选择：一是第一次只跳1级，此时跳法数目等于后面剩下的n-1级台阶的跳法数目，即为f(n-1);另一种选择是第一次跳2级，此时跳法数目等于后面剩下n-2级台阶的跳法数目，即为f(n-2)。因此，n级台阶的不同跳法的总数f(n)=f(n-1)+f(n-2)。分析到这里，不难看出这实际上就是斐波那契数列了。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

#include<iostream> using  namespace  std;     long  Fibonacci_Solution1(unsigned  int  n) {      if (n <= 0)          return  0;        if (n == 1)          return  1;        return  Fibonacci_Solution1(n - 1) + Fibonacci_Solution1(n - 2); }   int  main() {      int  n;      cin>>n;      cout<<Fibonacci_Solution1(n)<<endl;          return  0; }

 

 在青蛙跳台阶的问题中，如果把条件改成：一只青蛙一次可以跳上1级台阶，也可以跳上2级。。。。。它也可以跳上n级，此时该青蛙跳上一个n级的台阶总共有多少种跳法？

用数学归纳法可以证明f(n)=2^n-1.

 

本文转自夏雪冬日博客园博客，原文链接：http://www.cnblogs.com/heyonggang/p/3405089.html，如需转载请自行联系原作者