可持久化线段树(主席树)总结及板子

最新推荐文章于 2025-09-06 22:33:46 发布

weixin_33849942

最新推荐文章于 2025-09-06 22:33:46 发布

阅读量119

点赞数

CC 4.0 BY-SA版权

文章标签：数据结构与算法

原文链接：http://www.cnblogs.com/Hero-of-someone/p/7273862.html

本文详细介绍了主席树的原理及实现方法，包括如何构建、修改和查询主席树，并通过实例展示了其在解决区间k小值等问题上的应用。

　　不要问我为什么没学主席树就去做了 [BZOJ3065]带插入的区间k小值 ...我只想说我应该是一边写那道题一边学主席树一边学树套树的吧...好神奇哦,我居然还学会了...

　　有人讲我的博客就是全程在吐嘈,不仅没写什么有用的东西,还看不懂??!!! wtf??!! 好吧其实我就是在吐嘈,但至少你们看我的代码还是可以学会的好吧...

　　我又要开始 BB 了...

　　主席树跟普通的线段树其实也没什么区别嘛...建树也好,查询也好,修改也好,也就多那么一两行代码,而且也挺好理解的...

　　主席树其实也就是将线段树修改过程中的各个版本记录下来,将有修改痕迹的那一条链复制出来,并在修改后连接到原本的线段树上,如下图:

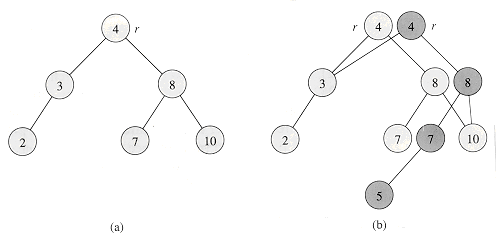
　　深色的点就是新版本中需要新建的点,浅色的 2,3,10 由于没有被修改,可以不用新建而是直接连接到新建的 8 上.这样的情况下,新建的点最多是 O(logn) 级别.

　　带操作的总复杂度的话: O(nlogn) .

　　下面讲讲怎么建树:

　　和线段树一样,递归建树,但主席树里的节点编号是没有提前确定的,需要动态开点.其余的和线段树一样:

il void build(RG int &x,RG int l,RG int r){
  t[++cnt]=t[x]; x=cnt;
  if(l==r){ t[x].sum=a[l]; return ; }
  RG int mid=(l+r)>>1;
  build(t[x].ls,l,mid),build(t[x].rs,mid+1,r);
  t[x].sum=t[ t[x].ls ].sum+t[ t[x].rs ].sum;
}

　　哇,有没有觉得贼简单.代码非常好懂有没有...

　　然后是修改和查询,单点修改和区间修改一起讲吧...

　　主席树里将标记可持久化是可以不用下放 lazy 的(当然线段树也可以这样做),只要在查询时计算一下每个节点 lazy 的贡献值就可以了,这个操作是我在做 UOJ#228基础数据结构 时从 ljh2000(%%%) 那学来的,,感觉常数一下小了好多hhh.　　

il void Modify(RG int &x,RG int l,RG int r,RG int L,RG int R,RG int v){
  t[++cnt]=t[x]; x=cnt;
  t[x].sum+=1ll*v*(R-L+1);//有了这个就可以不用递归更新父亲了
  if(l==L && r==R){ t[x].lazy+=v; return ; }
  RG int mid=(l+r)>>1;
  if(R<=mid) Modify(t[x].ls,l,mid,L,R,v);
  else if(L>mid) Modify(t[x].rs,mid+1,r,L,R,v);
  else{
    Modify(t[x].ls,l,mid,L,mid,v);
    Modify(t[x].rs,mid+1,r,mid+1,R,v);
  }
　//当然你也可以用递归的方式,看个人喜好吧
}

　　查询非常简单,就直接从你要查找的版本的跟开始,按线段树的流程查找就可以,如果修改时是像我一样的标记可持久化,别忘了加上 lazy

il ll Query(RG int x,RG int l,RG int r,RG int L,RG int R){
  if(L==l && r==R) return t[x].sum;
  RG int mid=(l+r)>>1; ll ans=t[x].lazy*(R-L+1);//计算 lazy 贡献
  if(R<=mid) ans+=Query(t[x].ls,l,mid,L,R);
  else if(L>mid) ans+=Query(t[x].rs,mid+1,r,L,R);
  else ans+=Query(t[x].ls,l,mid,L,mid)+Query(t[x].rs,mid+1,r,mid+1,R);
  return ans;
}

　　基本上操作就这样了,那什么...看不懂我在说什么的看代码也应该能看懂吧,代码真的很简洁了...希望对各位学主席树有帮助...

　　下面给一个完整的代码,是一道板子题.

　　Portal Gun:[HDU4348]To the Moon　　

#include<iostream>
#include<cstdio>
#include<cstdlib>
#define inf (1<<30)
#define maxn (100010)
#define ll long long 
#define il inline
#define RG register
using namespace std;
il int gi(){ RG int x=0,q=1; RG char ch=getchar(); while( ( ch<'0' || ch>'9' ) && ch!='-' ) ch=getchar();
  if( ch=='-' ) q=-1,ch=getchar(); while(ch>='0' && ch<='9') x=x*10+ch-48,ch=getchar(); return q*x; }

struct node{int ls,rs;ll sum,lazy;}t[maxn*30];
int n,m,cnt,num,root[maxn],a[maxn];
char op[10];

il void build(RG int &x,RG int l,RG int r){
  t[++cnt]=t[x]; x=cnt;
  if(l==r){ t[x].sum=a[l]; return ; }
  RG int mid=(l+r)>>1;
  build(t[x].ls,l,mid),build(t[x].rs,mid+1,r);
  t[x].sum=t[ t[x].ls ].sum+t[ t[x].rs ].sum;
}

il void Modify(RG int &x,RG int l,RG int r,RG int L,RG int R,RG int v){
  t[++cnt]=t[x]; x=cnt;
  t[x].sum+=1ll*v*(R-L+1);
  if(l==L && r==R){ t[x].lazy+=v; return ; }
  RG int mid=(l+r)>>1;
  if(R<=mid) Modify(t[x].ls,l,mid,L,R,v);
  else if(L>mid) Modify(t[x].rs,mid+1,r,L,R,v);
  else{
    Modify(t[x].ls,l,mid,L,mid,v);
    Modify(t[x].rs,mid+1,r,mid+1,R,v);
  }
}

il ll Query(RG int x,RG int l,RG int r,RG int L,RG int R){
  if(L==l && r==R) return t[x].sum;
  RG int mid=(l+r)>>1; ll ans=t[x].lazy*(R-L+1);
  if(R<=mid) ans+=Query(t[x].ls,l,mid,L,R);
  else if(L>mid) ans+=Query(t[x].rs,mid+1,r,L,R);
  else ans+=Query(t[x].ls,l,mid,L,mid)+Query(t[x].rs,mid+1,r,mid+1,R);
  return ans;
}

il void work(){
  while(~scanf("%d%d",&n,&m)){
    num=cnt=0; int x,y,v;
    for(int i=1;i<=n;i++) a[i]=gi();
    build(root[0],1,n);
    for(int i=1;i<=m;i++){
      scanf("%s",op);
      if(op[0]=='C'){
        x=gi(),y=gi(),v=gi(); ++num;
        Modify(root[num]=root[num-1],1,n,x,y,v);
      }
      if(op[0]=='Q'){
        x=gi(),y=gi();
        printf("%lld\n",Query(root[num],1,n,x,y));
      }
      if(op[0]=='H'){
        x=gi(),y=gi(),v=gi();
        printf("%lld\n",Query(root[v],1,n,x,y));
      }
      if(op[0]=='B') num=gi();
    }
  }
}

int main(){ work(); return 0; }

转载于:https://www.cnblogs.com/Hero-of-someone/p/7273862.html