[ZJOI2013]K大数查询

Description

有N个位置，M个操作。操作有两种，每次操作如果是1 a b c的形式表示在第a个位置到第b个位置，每个位置加入一个数c；
如果是2 a b c形式，表示询问从第a个位置到第b个位置，第C大的数是多少。

Input

第一行N，M。
接下来M行，每行形如1 a b c或2 a b c。

Output

输出每个询问的结果。

Sample Input

2 5
1 1 2 1
1 1 2 2
2 1 1 2
2 1 1 1
2 1 2 3

Sample Output

1
2
1

HINT

【样例说明】

第一个操作后位置1的数只有1，位置2的数也只有1。 第二个操作后位置1的数有1、2，位置2的数也有1、2。第三次询问位置1到位置1第2大的数是1。第四次询问位置1到位置1第1大的数是2。第五次询问位置1到位置2第3大的数是1。‍
N,M<=50000,N,M<=50000
a<=b<=N
1操作中|c|<=N
2操作中c<=Maxlongint

Source

思路

树套数，权值线段树套位置线段树。
如图：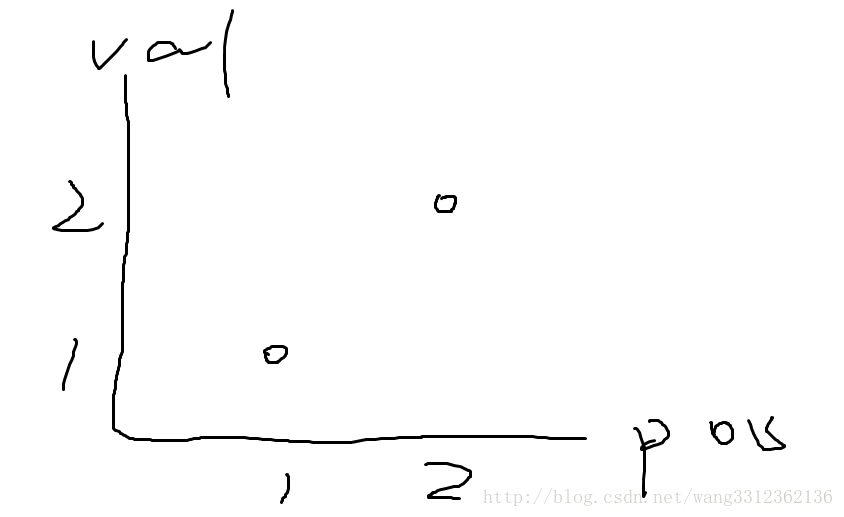

这个图表示1号位置有一个数1，2号位置有一个数2。
首先对纵坐标建立一棵线段树（权值线段树）；
再在权值线段树的每一个节点上对横坐标建立一棵线段树（位置线段树）；
插入操作（1 a b c）就是找到权值线段树上包含c这个点的区间，并将这些区间的线段树上[a,b]这个区间加上1。
查询操作（2 a b c）就是在权值线段树上查找对于[a,b]区间，刚好有[x,n]≥c且(x,n]>c的满足条件的x。

代码

（超大常数和超级扩行）

#include <cstdio>

const int maxn=50000;
const int maxs=20000000;

int n;

struct pos_segment_tree//位置线段树
{
  int ls[maxs],rs[maxs],cnt;
  unsigned val[maxs],lazy[maxs];

  inline int newnode()//为了节省空间，每访问一个节点再新建一个节点
  {
    ++cnt;
    ls[cnt]=rs[cnt]=val[cnt]=lazy[cnt]=0;
    return cnt;
  }

  inline int pushdown(int now,int left,int right)
  {
    if((!lazy[now])||(left==right))
      {
        return 0;
      }
    if(!ls[now])
      {
        ls[now]=newnode();
      }
    if(!rs[now])
      {
        rs[now]=newnode();
      }
    int mid=(left+right)>>1;
    val[ls[now]]+=lazy[now]*(mid-left+1);
    val[rs[now]]+=lazy[now]*(right-mid);
    lazy[ls[now]]+=lazy[now];
    lazy[rs[now]]+=lazy[now];
    lazy[now]=0;
    return 0;
  }

  inline unsigned updata(int now)
  {
    return val[now]=val[ls[now]]+val[rs[now]];
  }

  int add(int &now,int left,int right,int askl,int askr)
  {
    if(!now)
      {
        now=newnode();
      }
    pushdown(now,left,right);
    if((askl<=left)&&(right<=askr))
      {
        ++lazy[now];
        val[now]+=right-left+1;
        return 0;
      }
    int mid=(left+right)>>1;
    if(askl<=mid)
      {
        add(ls[now],left,mid,askl,askr);
      }
    if(mid<askr)
      {
        add(rs[now],mid+1,right,askl,askr);
      }
    updata(now);
    return 0;
  }

  unsigned query(int now,int left,int right,int askl,int askr)
  {
    if(!now)
      {
        return 0;
      }
    pushdown(now,left,right);
    if((askl<=left)&&(right<=askr))
      {
        return val[now];
      }
    int mid=(left+right)>>1;
    unsigned int res=0;
    if(askl<=mid)
      {
        res+=query(ls[now],left,mid,askl,askr);
      }
    if(mid<askr)
      {
        res+=query(rs[now],mid+1,right,askl,askr);
      }
    return res;
  }
};

struct val_segment_tree//权值线段树
{
  int root[maxn<<4];
  pos_segment_tree pst;

  int add(int now,int left,int right,int askl,int askr,int cv)
  {
    pst.add(root[now],1,n,askl,askr);
    if(left==right)
      {
        return 0;
      }
    int mid=(left+right)>>1;
    if(cv<=mid)
      {
        add(now<<1,left,mid,askl,askr,cv);
      }
    else
      {
        add(now<<1|1,mid+1,right,askl,askr,cv);
      }
    return 0;
  }

  int query(int now,int left,int right,int pl,int pr,unsigned int k)
  {
    if(left==right)
      {
        return left;
      }
    int mid=(left+right)>>1;
    unsigned int eq=pst.query(root[now<<1],1,n,pl,pr);
    if(eq>=k)
      {
        return query(now<<1,left,mid,pl,pr,k);
      }
    else
      {
        return query(now<<1|1,mid+1,right,pl,pr,k-eq);
      }
  }
};

val_segment_tree vst;
int m,opt,a,b,c;

int main()
{
  scanf("%d%d",&n,&m);
  while(m--)
    {
      scanf("%d%d%d%d",&opt,&a,&b,&c);
      if(opt==1)
        {
          vst.add(1,0,n<<1,a,b,n-c);
        }
      else
        {
          printf("%d\n",n-vst.query(1,0,n<<1,a,b,c));
        }
    }
  return 0;
}

转载于:https://www.cnblogs.com/Canopus-wym/p/10376256.html