车辆横向约束

车辆在行驶道路上存在曲率变化较大，如果不考虑横向约束执行机构转动速率的限制，可能造成车辆转角突然变大，导致车辆失稳，甚至侧翻。

为了保证车辆的横向稳定性需要对横向加以约束^[9]。

                                                                                                        

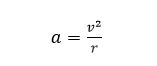
其中 表示车辆横向加速度， 表示车辆速度， 表示转弯半径， 与道路曲率 成倒数。本文不考虑车辆纵向控制，设定车辆在一定速度下，车道曲

率由车辆传感器给出，所以由式（7）可知当道路曲率变大时，车辆加速度会变小。由动力学关系求得：

                                                                           

                             

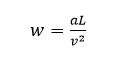
式中 为车辆转角，L为车辆轴距。由上面两个式子知车辆的转角可以随道路曲率变化，将 作为车辆在道路曲率 ，速度 给定条件下的最大转角

作为横向约束。

转载于:https://www.cnblogs.com/fuhang/p/8726969.html