最小二乘原理求解线性回归方程

在统计学中，线性回归(Linear Regression)是利用称为线性回归方程的最小平方函数对一个或多个 自变量和 因变量之间关系进行建模的一种 回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。只有一个自变量的情况称为简单回归,大于一个自变量情况的叫做多元回归。（这反过来又应当由多个相关的因变量预测的多元线性回归区别，[引文需要]，而不是一个单一的标量变量。）

回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为 多元线性回归分析。

在线性回归中，数据使用线性预测函数来建模，并且未知的模型参数也是通过数据来估计。这些模型被叫做线性模型。最常用的线性回归建模是给定X值的y的条件均值是X的仿射函数。不太一般的情况，线性回归模型可以是一个中位数或一些其他的给定X的条件下y的条件分布的分位数作为X的线性函数表示。像所有形式的回归分析一样，线性回归也把焦点放在给定X值的y的条件概率分布，而不是X和y的联合概率分布（多元分析领域）。

线性回归是回归分析中第一种经过严格研究并在实际应用中广泛使用的类型。这是因为线性依赖于其未知参数的模型比非线性依赖于其位置参数的模型更容易拟合，而且产生的估计的统计特性也更容易确定。

下面的例1 来自下面网址：

http://wenku.baidu.com/link?url=4Dlv5iuen0K9pb2rD-OICKRpXk0QrEcDjsbgJMXo0nuqIUHuq5im-HU8v6p3Q1QKvj0nEhzsV5znMH1V0Wa3WzDvvynNNd0rT8QCX8LKuwa

　　线性方程：y=bx+a ，r为相关系数。线性方程详情详细参考

http://baike.baidu.com/link?url=0Ob9UvB9oe01IXZj93iWNS8zbtqX1fSHdjK4JKB0w0jzmw_8C32U1H55HVWc7oYJ

　　

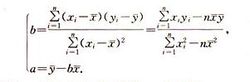
例1　10名同学在高一和高二的数学成绩如下表：

	74	71	72	68	76	73	67	70	65	74
	76	75	71	70	76	79	65	77	62	72

 

　　其中x为高一数学成绩，y为高二数学成绩．

　　（1）y与x是否具有相关关系；

　　（2）如果y与x是相关关系，求回归直线方程．

　　

c#程序实现：

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace testxyab
{
    class Program
    {
        static void Main(string[] args)
        {
           
            //数据来自上面的例子
            double[] x = new double[10] { 74,71,72,68,76,73,67,70,65,74};
            double[] y = new double[10] { 76,75,71,70,76,79,65,77,62,72};
            int count=10;
            double a,b,maxerr,rr;
            //a b 为系数，rr 为相关系数的平方，maxerr为最大偏差
            CalcRegress(x, y, count, out a, out b, out maxerr, out rr);
            Console.WriteLine("a={0}\n b={1}\n maxerr={2}\n rr={3}", a, b, maxerr, rr);
            Console.ReadKey();


        }
        public static void CalcRegress(double[] x, double[] y, int count, out double a, out double b, out double maxErr, out double r)
        {
            double sumX = 0;
            double sumY = 0;
            double avgX;
            double avgY;
            double r1;
            double r2;
//数据量过少，无法计算
            if (count < 4)
            {
               return;
            }

            for (int i = 0; i < count; i++)
            {
                sumX += x[i];
                sumY += y[i];
            }

            avgX = sumX / count;
            avgY = sumY / count;

            double SPxy = 0;
            double SSx = 0;
            double SSy = 0;
            for (int i = 0; i < count; i++)
            {
                SPxy += (x[i] - avgX) * (y[i] - avg_Y);
                SSx += (x[i] - avgX) * (x[i] - avgX);
                SSy += (y[i] - avg_Y) * (y[i] - avg_Y);
            }
//如果所有点的x相同，直线平行于y轴，无法计算。
//如果所有点的y相同直线为平行于x轴的直线y=k+0*x
            if (SSy==0)
            {
                a = y[1];
                b = 0;
                  rr=0;
            maxErr = 0;
                //return -1;
            }
            //y=bx+a
            b= SPxy / SSx;
            a= avgY - b* avgX;

            //开始计算R²值
            r1 = SPxy * SPxy;//分子的平方
            r2 = SSx * SSy;//分母的平方
            r = r1 / r2;    //计算R²值

            //下面代码计算最大偏差            
            maxErr = 0;
            for (int i = 0; i < count; i++)
            {
                double yi = a + b * x[i];
                double absErrYi = Math.Abs(yi - y[i]);//假动作

                if (absErrYi > maxErr)
                {
                    maxErr = absErrYi;
                }
            }
           
            
        }
    }
}