hdu6097 Mindis(几何）

最新推荐文章于 2018-07-07 18:15:00 发布

weixin_33815613

最新推荐文章于 2018-07-07 18:15:00 发布

阅读量71

点赞数

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/Saurus/p/7374662.html

本文介绍了一种通过解析几何的方法来解决特定类型的最值问题。利用椭圆和圆的位置关系，通过数学推导找到最优解。代码实现部分考虑了特殊情况下的处理方式。

题解：

这里是用解析解的做法，

我们发现如果以P和Q做椭圆，那么当椭圆与圆相切的时候，答案最优

那么方程就是这样的

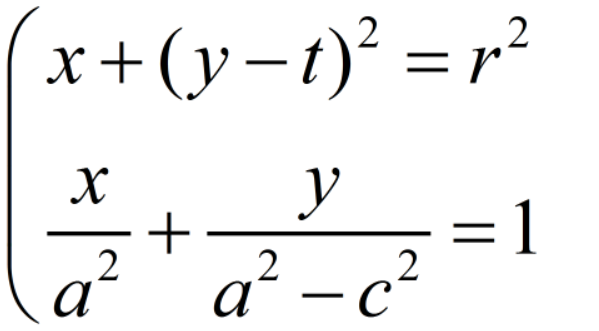
联立之后，解delta等于0，可以得到

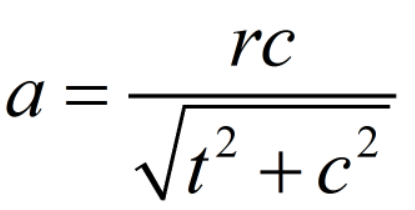
答案就是2a了

注意不一定任何情况都有解，当delta等于0时，不一定存在那个点，这个时候显然就为中垂线与圆的交点，特判一下即可

此外点重合也要特判！

#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
int T;
struct point{
    double x, y;
    point() { x = y = 0;}
    point(double _x, double _y):x(_x), y(_y) { }
}p[3];
const double eps = 1e-8;
double dis(point A, point B){
    return sqrt(pow(A.x - B.x, 2)+pow(A.y - B.y, 2));
}
double r, c, t, a;
int main()
{
    cin>>T;
    while(T--){
        scanf("%lf%lf%lf%lf%lf",&r,&p[1].x,&p[1].y,&p[2].x,&p[2].y);
        c = dis(p[1], p[2])/2;
        t = sqrt(pow(dis(p[1], p[0]), 2) - c*c);
        a = r*c/sqrt(t*t+c*c);
        if(abs(c) < eps){
            point C = point(c, 0);
            point D = point(0, -r+t);
            printf("%.10f\n", 2*dis(C, D));
            continue;
        }
        if(abs(a - c) < eps) {
            printf("%.10f\n", 2*a);
            continue;
        }
        double B = 2*t*(a*a-c*c);
        double A = c*c;
        double Y = -B/A/2;
        if((Y-t)*(Y-t) - r*r > eps){
            point C = point(c, 0);
            point D = point(0, -r+t);
            printf("%.10f\n", 2*dis(C, D));
        } else {
            printf("%.10f\n", 2*a);
        }
    }
}

转载于:https://www.cnblogs.com/Saurus/p/7374662.html