dp-多重背包

最新推荐文章于 2025-07-27 20:40:58 发布

转载最新推荐文章于 2025-07-27 20:40:58 发布 · 85 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/ccut-ry/p/7365791.html

本文详细介绍了多重背包问题的解决方法，包括使用二维数组实现的基本算法和采用二进制思想进行优化的方法。此外还提供了具体的代码示例，帮助读者更好地理解和应用多重背包算法。

（推荐： http://blog.youkuaiyun.com/insistgogo/article/details/11176693 ）

学会了前两个背包，学这个背包还是很轻松的。

　　多重背包，顾名思义，就是前两种背包结合到一起，首先还是用一个例子说明。

1、问题描述

　　已知:有一个容量为V的背包和N件物品，第i件物品最多有Num[i]件，每件物品的重量是weight[i]，收益是cost[i]。

　　问题:在不超过背包容量的情况下，最多能获得多少价值或收益

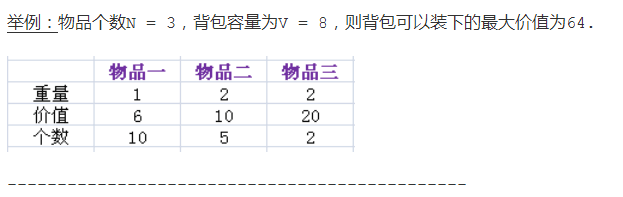
多重背包区别于二重背包的地方就在于所给出的物品数是有限的。

　　用二维数组写出代码：

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std ;
#define Max(a,b) a>b?a:b
#define Min(a,b) a>b?b:a

int dp[100][1000] ;
int weight[10] ;
int value[10] ;
int num[10] ;

int main ( ) {
    int n , v ;
    cin >> n >> v ;

    for ( int i = 1 ; i <= n ; i++ ) {
        cin >> weight[i] >> value[i] >> num[i] ;
    }

    for ( int i = 1 ; i <= n ; i++ ) {
        for ( int j = weight[i] ; j <= v ; j++ ) {
            int f = Min ( num[i] , j / weight[i] ) ;
            for (int k = 1 ; k <= f ; k*=2 ) {    // 三层 for ， 最内层的for 用来进行在进行在 每种物品的每种体积下，一直放入同一种物品
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　// 此处有一个小的优化 ， 就是我每种物品的数量通过 1、2、4、8、16……2^k 来控制 
                dp[i][j] = Max ( dp[i-1][j] , dp[i-1][j-k*weight[i]]+k*value[i] ) ;
            //    cout << dp[i][j] << '\t' ;
            }

        }
    //    cout << '\n' ;
    }

    cout << dp[n][v] << endl ;
    return 0 ;
}

上述的优化方法就采用了二进制的思想

　　对每件物品拆分，拆分的数量可以是 1件、 2件、 4件 ……2^k 件，并且要保证 2^k <= num[ i ] ，但是这里的最后一件是 num[ i ] - 前面所有物品的和，那么对 num[ i ] 来说，就一定会有前面的数相加等于 num[ i ] ，其实这样对物品拆分，在取得话，就可以看成每件新拆分出的物品只有一件，进而不就转换成 01背包了吗，一定要注意领悟这个拆分的思想，是讲背包的物品总数分解开。

优化：

　　说到拆分，有种情况是不用拆分的，就是当 weight[ i ] * num[ i ] >= v ，因为这种情况就可以理解成物品的数量充足，那么不就转化成完全背包的情况吗？直接就会被优化到 O（v*n）。

　　对于不满足完全背包情况的物品进行拆分，此时物品的个数就没有对所有物品进行拆分的个数多，那么循环的次数就会降下来，复杂度也就降低了。

代码示例：

#include <iostream>  
using namespace std;  
  
const int N = 3;//物品个数  
const int V = 8;//背包容量  
int Weight[N + 1] = {0,1,2,2};  
int Value[N + 1] = {0,6,10,20};  
int Num[N + 1] = {0,10,5,2};  
  
int f[V + 1] = {0};  
/* 
f[v]:表示把前i件物品放入容量为v的背包中获得的最大收益。 
f[v] = max(f[v],f[v - Weight[i]] + Value[i]); 
v的为逆序 
*/  
void ZeroOnePack(int nWeight,int nValue)  
{  
    for (int v = V;v >= nWeight;v--)  
    {  
        f[v] = max(f[v],f[v - nWeight] + nValue);  
    }  
}  
  
/* 
f[v]:表示把前i件物品放入容量为v的背包中获得的最大收益。 
f[v] = max(f[v],f[v - Weight[i]] + Value[i]); 
v的为增序 
*/  
void CompletePack(int nWeight,int nValue)  
{  
    for (int v = nWeight;v <= V;v++)  
    {  
        f[v] = max(f[v],f[v - nWeight] + nValue);  
    }  
}  
  
int MultiKnapsack()  
{  
    int k = 1;  
    int nCount = 0;  
    for (int i = 1;i <= N;i++)  
    {  
        if (Weight[i] * Num[i] >= V)  
        {  
            //完全背包:该类物品原则上是无限供应，  
            //此时满足条件Weight[i] * Num[i] >= V时，  
            //表示无限量供应，直到背包放不下为止.  
            CompletePack(Weight[i],Value[i]);  
        }  
        else  
        {  
            k = 1;  
            nCount = Num[i];  
            while(k <= nCount)  
            {  
                ZeroOnePack(k * Weight[i],k * Value[i]);  
                nCount -= k;  
                k *= 2;  
            }  
            ZeroOnePack(nCount * Weight[i],nCount * Value[i]);  
        }  
    }  
    return f[V];  
}  
  
int main()  
{  
    cout<<MultiKnapsack()<<endl;  
    system("pause");  
    return 1;  
}

转载于:https://www.cnblogs.com/ccut-ry/p/7365791.html