本文探讨了多种几何图形如何通过特定的方式拼接成正方形或矩形，并最终得出波尔约-格维也纳定理，即任意两个面积相等的多边形可以相互拼接。文章还介绍了拼接过程中的一系列有趣结论。
今天看到《思维的乐趣》关于拼接的数学，挺有意思，写下来。
结论1：任意两个正方形，可以拼接成一个大正方形。如图
结论2：任意多个正方形都可以拼接成一个大正方形。
证明：滚雪球，拿两个一拼，然后完了再拿两个一拼。最后就剩一个大正方形。
结论3：如果图形A能拼接成图形B，图形B能拼接成图形C，则图形A也能拼接成图形C。
结论4：如果图形A能拼接成图形B，则图形B也能拼接成图形A。
结论5：若矩形的长宽之比小于4:1，则这个矩形可以拼接成正方形。
结论6：任意一个长宽之比超过4:1的矩形都能拼接成一个长宽比小于4:1的矩形。
结论7：由5、6推出，任意一个矩形可以拼接成一个正方形。
结论8：任意一个平行四边形都可以拼接成一个矩形。如图
结论9：任意一个三角形都能拼接成一个平行四边形。如图
结论10：任意一个四边形都可以拼接成一个正方形（以为任意一个四边形都可以又若干三角形组成）。
结论11：任意一个多边形都可以拼接成一个正方形（理由同上）。如图
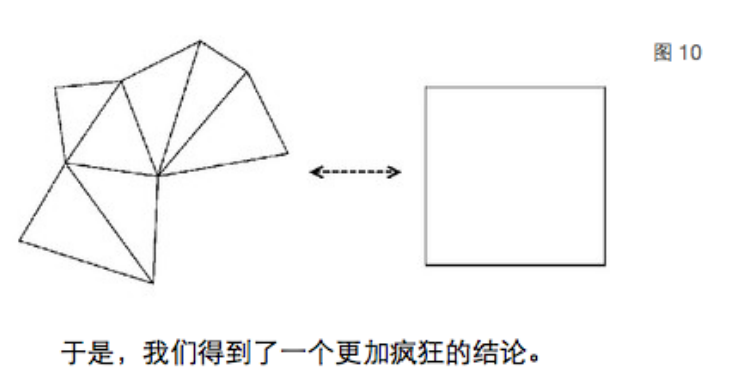
最终得到结论12，即就是波尔约-格维也纳定理：
任意两个面积相等的多边形，它们可以相互拼接得到。
由法卡斯·波尔约(Farks Bolyai)和保罗·格维也纳(Paul Gerwien)两位数学家分别在1833年和1835年证明。
扫一扫
808
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
