将三角形绕点b顺时针旋转90度_【同步练习】九年级数学上册23.1 图形的旋转（1）...

一、单选题(共12小题，每小题2分，共24分)

1、下列现象：①时针转动；②荡秋千；③转呼啦圈；④传送带上电视机的运动．其中属于旋转的有(   )  

A、①②B、②③C、①④D、③④

正确答案

A

解析

解：①时针转动，是旋转现象；

②荡秋千，是旋转现象；

③转呼啦圈,不是旋转现象；

④传送带上电视机的运动，是平移现象.

属于旋转的有①②．

故答案为：A．

2、用数学的方式理解“两岸猿声啼不住，轻舟已过万重山”和坐地日行八万里”(只考虑地球的转)，

其中蕴含的图形运动是(     )．

A、平移和旋转B、对称和旋转C、对称和平移D、旋转和平移

正确答案

A

解析

解：根据平移和旋转定义：“两岸猿声啼不住，轻舟已过万重山”是平移；“坐地日行八万里”是旋转．故答案为：A

3、如图，小林坐在秋千上，秋千旋转了80°，小林的位置也从A点运动到了A'点，则∠OAA'的度数为(   )

A、40°B、50°C、70°D、80°

正确答案

B

解析

解：∵秋千旋转了80°，小林的位置也从A点运动到了A'点，  ∴AOA′=80°，OA=OA′，

∴∠OAA'=(180°﹣80°)=50°．

故选：B．

4、如图，在正方形网格中，线段A′B′是线段AB绕某点逆时针旋转角α得到的，点A′与A对应，则角α的大小为(   )

A、30°B、60°C、90°D、120°

正确答案

C

解析

解：如图，连接A′A，BB′，分别A′A，BB′作的中垂线，相交于点O.

显然，旋转角为90°，

故答案为：C

5、等边三角形与它本身重合，需绕着它的三边中线的交点旋转至少(    ).

A、60°B、180°C、360°D、120°

正确答案

D

解析

如下图，△ABC为等边三角形，点O为三边中线的交点，那么∠EOG=∠GOF=∠EOF，所以△ABC旋转120°即可与本身重合．

6、如图，将直角三角形ABC向右翻滚，下列说法正确的有(   )

( 1 )①②是旋转；(2)①③是平移；(3)①④是平移；(4)②③是旋转．

A、1种B、2种C、3种D、4种

正确答案

C

解析

(1)①到②是△ABC绕点C顺时针旋转90°所得，此结论正确；(2)①到③不是平移，此结论错误；(3)①到④是△ABC沿AC方向平移C′C″距离所得，此结论正确；(4)②到③是△ABC绕点B′顺时针旋转∠A′B′A″的大小所得，此结论正确；故答案为：C．

7、如图,选项中的四个三角形不能由△ABC经过旋转或平移得到的是(   )

A、 B、 C、 D、

正确答案

B

解析

解：A、图形由原图形平移得到，故A正确；
B、图形由原图形轴对称得到，故B错误；
C、图形由原图形旋转得到，故C正确；
D、图形由原图形旋转得到，故D正确；
故选：B．

8、下列图案中，可以由一个”基本图案”连续旋转45°得到的是(   )   

A、 B、 C、 D、

正确答案

B

解析

解：根据旋转的性质可知，可以由一个“基本图案”连续旋转45°，即经过8次旋转得到的是B．故答案为：B

9、如图所示，把菱形ABOC(四条边都相等)绕点O顺时针旋转得到菱形DFOE，则下列角中，不是旋转角的为(    )

A、∠BOFB、∠AODC、∠COED、∠AOF

正确答案

D

解析

两对应边所组成的角都可以作为旋转角，结合图形即可得出：

A、OB旋转后的对应边为OF，故∠BOF可以作为旋转角，不符合题意；

B、OA旋转后的对应边为OD，故∠AOD可以作为旋转角，不符合题意；

C、OC旋转后的对应边为OE，故∠COE可以作为旋转角，不符合题意；

D、OA旋转后的对应边为OD不是OF，故∠AOF不可以作为旋转角，符合题意；

故答案为：D．

10、如图，若正方形EFGH由正方形ABCD绕某点旋转得到，则可以作为旋转中心的是(　　)

A、M或O或NB、E或O或CC、E或O或ND、M或O或C

正确答案

A

解析

若以M为旋转中心，把正方形ABCD顺时针旋转90°，A点对应点为H，B点对应点为E，C点对应点为F，D点对应点为G，则可得到正方形EFGH；

若以O为旋转中心，把正方形ABCD旋转180°，A点对应点为G，B点对应点为H，C点对应点为E，D点对应点为F，则可得到正方形EFGH；

若以N为旋转中心，把正方形ABCD逆时针旋转90°，A点对应点为F，B点对应点为G，C点对应点为H，D点对应点为E，则可得到正方形EFGH．

故选A．

11、在下列四种图形变换中，图案包含的变换是(   )

A、旋转和轴对称B、轴对称和平移C、平移和旋转D、平移、旋转和轴对称

正确答案

A

解析

此图案是中心对称图形又是轴对称图形，所以包含的变换是旋转和轴对称.故答案为：A

12、如图，将线段AB绕点O顺时针旋转90°得到线段A′B′，那么A(﹣2，5)的对应点A′的坐标是(   )

A、(5，2) B、(2，5)C、(2，﹣5)D、(5，﹣2)

正确答案

A

解析

作AD⊥x轴于点D，作A′D′⊥x轴于点D′，

则OD=A′D′，AD=OD′，OA=OA′，

∴△OAD≌△A′OD′(SSS)，

∵A(-2，5)，

∴OD=2，AD=5，

∴点A′的坐标为(5，2)，

故答案为：A．

二、填空题(共5小题，每小空4分，共28分)

13、(8分)图形的旋转只改变图形的            ，而不改变图形的            .

正确答案

位置，形状和大小

解析

根据图形的旋转的性质，可知图形的旋转只改变图形的位置，而不改变图形的形状和大小.

14、(8分)正六边形可以看成由基本图形           经过           次旋转而成．    

正确答案

正三角形；5

解析

根据图形可得：正六边形可以看成由基本图形正三角形经过5次旋转而成．

15、(4分)如图所示，在正方形网格中，图①经过旋转得到图②，其旋转中心是点           (填“A”“B”“C”或“D”)．

正确答案

A

解析

如图：

分别连接两组对应点，作它们的垂直平分线a，和b，

∵直线a、b交于点A．

∴旋转中心就是点A．

故答案为：A

16、(4分)钟表上的指针随时间的变化而移动，这可以看作是数学上的           .    

正确答案

旋转

解析

根据钟表的指针绕一点旋转变化得到时间的变化，因此我们可以看作是数学上的旋转.

17、(4分)如图，在6×4方格纸中，格点三角形甲经过旋转后得到格点三角形乙，则其旋转中心是             ．  

正确答案

点N

解析

解：如图，连接N和两个三角形的对应点；  

发现两个三角形的对应点到点N的距离相等，因此格点N就是所求的旋转中心.

三、解答题(共5小题，共48分)

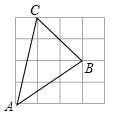
18、(12分)如图，AC是正方形ABCD的对角线，△ABC经过旋转后到达△AEF的位置．

(1)指出它的旋转中心；    

(2)说出它的旋转方向和旋转角是多少度；    

(3)分别写出点A，B，C的对应点．    

正确答案

(1)它的旋转中心为点A

(2)它的旋转方向为逆时针方向，旋转角是45度

(3)点A，B，C的对应点分别为点A，E，F 

解析

解：(1)通过观察发现△ABC绕着点A经过旋转后到达△AEF的位置；

(2)通过观察发现△ABC绕着点A沿逆时针方向旋转45º后到达△AEF的位置；

(3)△ABC绕着点A沿逆时针方向旋转45º后到达△AEF的位置后，点A是旋转中心没有动，故其对应点还是点A，点B转到了点E的位置，点C转到了点F的位置。

19、(6分)四边形ABCD是正方形，E、F分别是DC和CB的延长线上的点，且DE=BF，连接AE、AF

(1)求证：△ADE≌△ABF．    

(2)填空：△ABF可以由△ADE绕旋转中心          点，按顺时针方向旋转          度得到．   

正确答案

见解析

解析

(1)证明：∵四边形ABCD是正方形，

∴AD=AB，∠D=∠ABC=90°，

而F是CB的延长线上的点，

∴∠ABF=90°，

在△ADE和△ABF中，

，

∴△ADE≌△ABF(SAS)

(2)△ABF可以由△ADE绕旋转中心点A，按顺时针方向旋转90度得到．

20、(6分)平面直角坐标系中，有一Rt△ABC，且A(﹣1，3)，B(﹣3，﹣1)，C(﹣3，3)，已知△A1AC1是由△ABC旋转得到的．

(1)请写出旋转中心的坐标是              ，旋转角是              度；    

(2)以(1)中的旋转中心为中心，分别画出△A₁AC₁顺时针旋转90°、180°的三角形．

正确答案

见解析

解析

解：(1)旋转中心的坐标是(0，0)，旋转角是90度；

(2)解：如图所示，△A₁A₂C₂是△A₁AC₁以O为旋转中心，顺时针旋转90°的三角形，

△A₂C₃B是△A₁AC₁以O为旋转中心，顺时针旋转180°的三角形．

21、(12分)如图，钟表的分针匀速旋转一周需要60分钟，那么：

(1)它的旋转中心是什么？    

(2)分针旋转一周，时针旋转多少度？    

(3)上午8点整，时针和分针的夹角是多少？8点半呢？

正确答案

见解析

解析

(1)解：它的旋转中心是表盘中心

(2)解：分针旋转一周，时针旋转30度，因为一圈为360度，而一圈为12小时，所以一小时就是360度除以12，即一小时为30度

(3)解：8点整，时针指向8，分针指向12，钟表12个数字，每相邻两个数字之间的夹角为30°，

因此8点整分针与时针的夹角正好是4×30°=120°；

8点半：时针与分针的夹角为：30°×8+0.5°×30-6°×30=75° 。

22、(12分)在如图所示的方格纸中，每个小方格都是边长为1个单位的正方形，图①、图②、图③均为顶点都在格点上的三角形(每个小方格的顶点叫格点)，

(1)在图1中，图①经过一次           变换(填“平移”或“旋转”或“轴对称”)可以得到图②；    

(2)在图1中，图③是可以由图②经过一次旋转变换得到的，其旋转中心是点           (填“A”或 “B”或“C”)；    

(3)在图2中画出图①绕点A顺时针旋转90°后的图④.    

正确答案

(1)平移

(2)A

(3)解：如图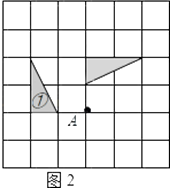

解析

解：

(1)因为平移不会改变图形的方向和大小，图①与图②只是改变了图形的位置，方向大小都没有改变，故图①经过一次平移变换可以得到图②；

(2)旋转的性质，每对对应点到旋转中心的距离相等，即旋转中心在每对对应点所连线段的中垂线上，旋转前后的图形大小形状都不会改变，但位置和方向会改变，根据性质即可得出图③是可以由图②经过一次旋转变换得到的，其旋转中心是点A；

(3)利用网格纸的特点及旋转的性质，画出图①各个顶点绕点A顺时针旋转 90 ∘ 得到的对应点再顺次连接即可得到所求的图形④。

声明：本公众号尊重知识产权，素材来源于网络，若有侵权请联系删除。

关注我，获取更多资料