1.题目要求
最大连续子数组和(最大子段和)
问题描述: 给定n个整数(可能为负数)组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0,依此定义,所求的最优值为: Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如,当(a[1],a[2],a[3],a[4],a[5],a[6])=(-2,11,-4,13,-5,-2)时,最大子段和为20。
2.程序设计
| 2.1程序设计思想:(动态规划思想) |
状态方程 : max( dp[ i ] ) = getMax( max( dp[ i -1 ] ) + arr[ i ] ,arr[ i ] )
上面式子的意义是:我们从头开始遍历数组,遍历到数组元素 arr[ i ] 时,连续的最大的和 可能为 max( dp[ i -1 ] ) + arr[ i ] ,也可能为 arr[ i ] ,做比较即可得出哪个更大,取最大值。时间复杂度为 n。
| 2.2程序代码 |
#include<iostream>
using namespace std;
int GetMax(int a, int b) //得到两个数的最大值
{
return (a) > (b) ? (a) : (b);
}
int GetMaxAddOfArray(int* arr, int sz)
{
if (arr == NULL || sz <= 0)
return 0;
int tem = 0;
for (int i = 0; i < sz; i++)
{
if (arr[i] < 0)
tem++;
}
if (tem == sz)
return 0;
else
{
int Sum = arr[0]; //临时最大值
int MAX = arr[0]; //比较之后的最大值
for (int i = 1; i < sz; i++)
{
Sum = GetMax(Sum + arr[i], arr[i]); //状态方程
if (Sum >= MAX)
MAX = Sum;
}
return MAX;
}
}
int main()
{
int array[] = { -1,-3,4,6,-2,6,-1,0 };//2, 3, -6, 4, 6, 2, -2, 5, -9
int sz = sizeof(array) / sizeof(array[0]);
int MAX = GetMaxAddOfArray(array, sz);
cout << MAX << endl;
return 0;
}3.测试程序
| 3.1逻辑图的设计 |
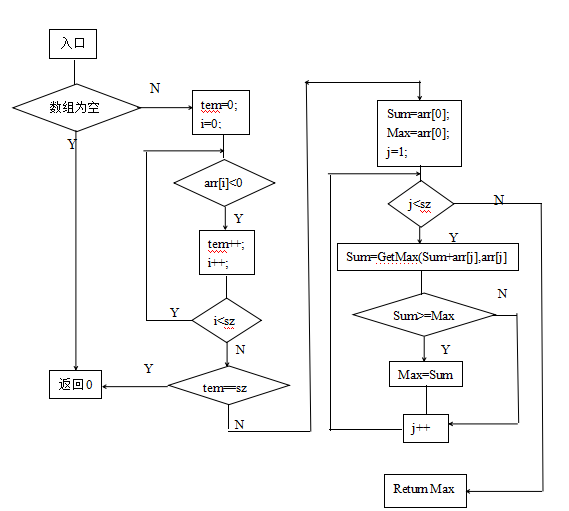
| 3.2判定/条件覆盖测试 |
| First | Second | Third | Fourth | Fifth | Sixth |
|---|---|---|---|---|---|
| arr数组为空 | arr[i]<0 | i<sz | tem==sz | j<sz | Sum>=Max |
| arr数组不为空 | arr[i]>=0 | i>=sz | tem!=sz | j>=sz | Sum<Max |
| 3.3样例的选择 |
3.3.1
样例1:arr{};
3.3.2
样例2:arr{4}={-1,-2,-3,-4};
3.3.3
样例3:arr{8}={-1,-3,4,6,-2,6,-1,0};
| 3.4测试程序代码 |
#include <stdafx.h>
#include <CppUnitTest.h>
extern int GetMaxAddOfArray(int* arr, int sz);
using namespace Microsoft::VisualStudio::CppUnitTestFramework;
namespace UnitTest1
{
TEST_CLASS(UnitTest1)
{
public:
TEST_METHOD(TestMethod1)
{
int *array = {};
int sz = sizeof(array) / sizeof(array[0]);
int Max=GetMaxAddOfArray(array,sz);
Assert::AreEqual(Max,0);
}
TEST_METHOD(TestMethod2)
{
int array[]= { -1,-2,-3,-4 };
int sz = sizeof(array) / sizeof(array[0]);
int Max = GetMaxAddOfArray(array,sz);
Assert::AreEqual(Max,0);
}
TEST_METHOD(TestMethod3)
{
int array[]= { -1,-3,4,6,-2,6,-1,0 };
int sz = sizeof(array) / sizeof(array[0]);
int Max = GetMaxAddOfArray(array,sz);
Assert::AreEqual(Max,14);
}
};
}4.测试结果
测试结果一开始由于对数据设置的出错导致其中有一个测试样例出错,如下图所示: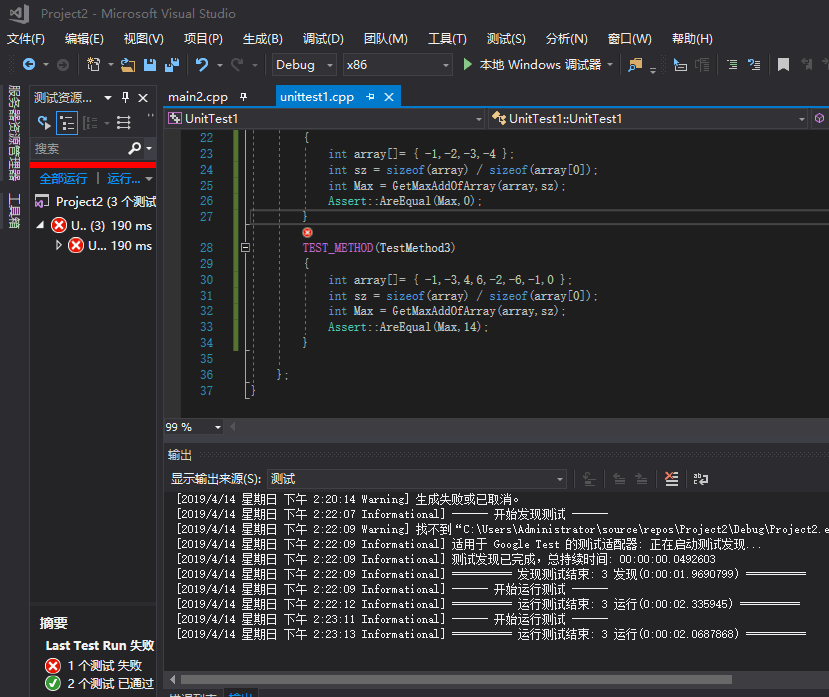
后来经更正三组测试用例全部通过,如下图所示: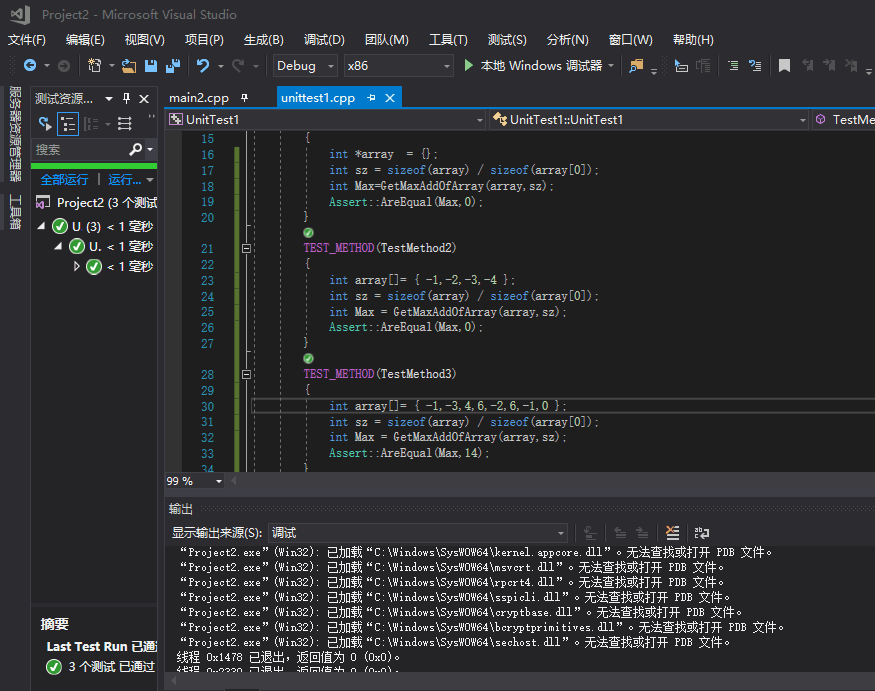
5.心得体会
| It is obvious that:A little care in each step will shorten the time and improve the efficiency! |







 本文详细解析了最大连续子数组和(最大子段和)问题的解决方法,采用动态规划思想,阐述了状态方程及其意义,并提供了具体实现代码与测试案例。
本文详细解析了最大连续子数组和(最大子段和)问题的解决方法,采用动态规划思想,阐述了状态方程及其意义,并提供了具体实现代码与测试案例。
















 1954
1954

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








