排序算法总结

2019独角兽企业重金招聘Python工程师标准>>>

一、选择排序

        思想：先筛选出一个当前结点以后所有结点中的最小值，然后替换当前结点，刚开始排序很慢，随着时间推移，排序速度越来越快。

        性能：速度表现稳定

二、插入排序

       思想：遍历结点，将当前结点放入序列中的恰当位置，刚开始排序很快，随着时间推移，排序速度越来越慢。

       性能：如果序列大致呈顺序排列，性能将快于选择排序

三、 归并排序

#include <stdio.h>
#include <stdlib.h> // rand sranddev

#define DEBUG 1
#define SORT_NUM 10

void print_array( int *list, int len);
void merge_array( int *list1, int list1_size, int *list2, int list2_size);

/**
 * @brief 归并排序
 *
 * @param *list 要排序的数组
 * @param n 数组中的元素数量
 */
void merge_sort( int *list, int list_size)
{
    if (list_size > 1)
    {
        // 把数组平均分成两个部分
        int *list1 = list;
        int list1_size = list_size / 2;
        int *list2 = list + list_size / 2;
        int list2_size = list_size - list1_size;
        // 分别归并排序
        merge_sort(list1, list1_size);
        merge_sort(list2, list2_size);

        // 归并
        merge_array(list1, list1_size, list2, list2_size);
    }
}

/**
 * @brief 归并两个有序数组
 *
 * @param list1
 * @param list1_size
 * @param list2
 * @param list2_size
 */
void merge_array( int *list1, int list1_size, int *list2, int list2_size)
{
    int i, j, k;
    i = j = k = 0;

    // 声明临时数组用于存储归并结果
    int list[list1_size + list2_size];

    // note: 只要有一个数组到达了尾部就要跳出
    // 也就是说只有两个都没有到达尾部的时候才执行这个循环
    while (i < list1_size && j < list2_size)
    {
        // 把较小的那个数据放到结果数组里， 同时移动指针
        list[k++] = list1[i] < list2[j] ? list1[i++] : list2[j++];
    }

    // 如果 list1 还有元素，把剩下的数据直接放到结果数组
    while (i < list1_size)
    {
        list[k++] = list1[i++];
    }

    // 如果 list2 还有元素，把剩下的数据直接放到结果数组
    while (j < list2_size)
    {
        list[k++] = list2[j++];
    }

    // 把结果数组 copy 到 list1 里
    for ( int ii = 0; ii < (list1_size + list2_size ); ++ii)
    {
        list1[ii] = list[ii];
    }

}

/**
 * @brief 打印数组
 *
 * @param list[]
 * @param len
 */
void print_array( int *list, int len)
{
    int i;
    for (i = 0; i < len; ++i)
    {
        // printf ("%3d", *(list+i));
        printf("%3d" , list[i]);
        if (i < len - 1)
            printf(" " );
    }
    printf( "\n");
}

int main( void)
{
    int len = SORT_NUM;
    int list[len];
    for ( int i = 0; i < len; ++i)
    {
        sranddev();
        list[i] = rand() % (SORT_NUM * SORT_NUM);
    }

    print_array(list, len);
    merge_sort(list, len);
    print_array(list, len);

    return 0;
}

     归并排序思想是，将序列分散到颗粒最小的时候，然后重组(明显的递归思维)；和之前排序算法不同，这个会占用空间，这也就是计算机中，空间置换时间的思想。

     归并排序算法时间复杂度：假设一共有n个元素，那么归并树层次为log2n，当然可以也为lgn。

     换种理解思路，假设一共有n个元素，二分法递归次数则为log2n，这个正好也是其排序算法的运算步数。

     每一层的工作量为n，所以时间复杂度为O(nlgn)

四、快速排序

#include <stdio.h>
int a[] = { 1, 2, 8, 7, 9, 5, 6, 4, 3, 66, 77, 33, 22, 11 };

/* 输出数组前n各元素 */
void prt(int n)
{
    int i;
    for (i = 0; i < n; i++)
   {
        printf("%d\t" , a[i]);
    }
    printf( "\n");
}

/* 数据交换 */
inline void swap( int *a, int *b)
{
    int tmp;
    tmp = *a; *a = *b; *b = tmp;
}

void quick_sort( int a[], int left, int right)
{
    int i = left + 1, j = right;
    int  key = a[left];//将最左边元素作为key值，这里注意，将最左边元素作为key值并不是最好选择，应该去中间元素比较合适
    if (left >= right) return;
    /* 从i++和j--两个方向搜索不满足条件的值并交换  *
     * 条件为：i++方向小于key，j--方向大于key      */
    while (1)
    {
       /*寻找参照物，将首元素作为参照物key，筛选，如果a[i]比key大，a[j]比key小的话，此时a[i]和a[j]相互交换*/
       while (a[j ] > key)
          j--;
       while (a[i] < key&&i< j)
          i++;
       /*找到key的位置，也就是所谓的标杆，中止循环 */
       if(i >= j )
          break;
       swap(&a[i],&a[ j]);
       if(a[i]==key)
           j--;
       else
           i++;
    }
    /* 关键数据放到‘中间’ */
    swap(&a[left],&a[j ]);
    if(left  < i - 1)   quick_sort(a, left, i - 1);
    if(j + 1 < right)  quick_sort(a, j + 1 , right);
}

int main( void) {
    /* 排序与输出 */
    quick_sort(a, 0, 13);
    prt(14);
    return 0;
}

思想：分治法

1．先从数列中取出一个数作为基准数key。

2．分区过程，将比这个数大的数全放到基准数的右边，小于或等于它的数全放到基准数的左边，在此过程中，基准数也是不断调整和改变的，直到i>=j的时候，才能将基准数key确定下来，并同时也确定了具体的位置。

3．再对key左右区间重复第二步，直到各区间只有一个数。完成排序。

4．最坏情况是已经排序好的序列需要非常长的时间去检验

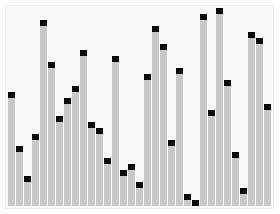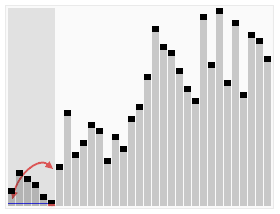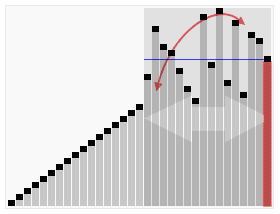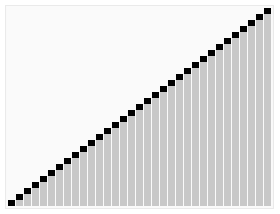
平均时间复杂度依然是O(nlog2n)

五、堆排序（Heap Sort）

#include <cstdio>
#include <cstdlib>
#include <cmath>
using namespace std;
 
int parent(int);
int left(int);
int right(int);
void Max_Heapify(int [], int, int);
void Build_Max_Heap(int [], int);
void print(int [], int);
void HeapSort(int [], int);
 
/*父結點*/
int parent(int i)
{
    return (int)floor((i - 1) / 2);
}
 
/*左子結點*/
int left(int i)
{
    return (2 * i + 1);
}
 
/*右子結點*/
int right(int i)
{
    return (2 * i + 2);
}
 
/*單一子結點最大堆積樹調整*/
void Max_Heapify(int A[], int i, int heap_size)
{
    int l = left(i);
    int r = right(i);
    int largest;
    int temp;
    if(l < heap_size && A[l] > A[i])
    {
        largest = l;
    }
    else
    {
        largest = i;
    }
    if(r < heap_size && A[r] > A[largest])
    {
        largest = r;
    }
    if(largest != i)
    {
        temp = A[i];
        A[i] = A[largest];
        A[largest] = temp;
        Max_Heapify(A, largest, heap_size);
    }
}
 
/*建立最大堆積樹*/
void Build_Max_Heap(int A[]，int heap_size)
{
    for(int i = (heap_size-2)/2; i >= 0; i--)
    {
        Max_Heapify(A, i, heap_size);
    }
}
 
/*印出樹狀結構*/
void print(int A[]， int heap_size)
{
    for(int i = 0; i < heap_size;i++)
    {
        printf("%d ", A[i]);
    }
    printf("\n");
}
 
/*堆積排序程序碼*/
void HeapSort(int A[], int heap_size)
{
    Build_Max_Heap(A, heap_size);
    int temp;
    for(int i = heap_size - 1; i >= 0; i--)
    {
        temp = A[0];
        A[0] = A[i];
        A[i] = temp;
        Max_Heapify(A, 0, i);
    }
    print(A, heap_size);
}
 
/*輸入資料並做堆積排序*/
int main(int argc, char* argv[])
{
    const int heap_size = 13;
    int A[] = {19, 1, 10, 14, 16, 4, 7, 9, 3, 2, 8, 5, 11};
    HeapSort(A, heap_size);
    system("pause");
    return 0;
}

其实堆排序的思想就是不断找到一个标杆，即是整个序列的最大值，放到根结点，然后从最尾部和根结点比对，然后周而复始继续寻找下一个标杆。。。。。从而从尾至头逐一确定每个成员的位置，完成排序！

转载于:https://my.oschina.net/leonwong1121/blog/211733