梯度消失和梯度爆炸

1.原因

  神经网络为什么会出现梯度消失和梯度爆炸的问题，根源是反向传播。一般整个深度神经网络可以视为一个复合的非线性多元函数

  那么在这样一个公式中，我们都知道，计算梯度的时候是链式求导，比如一个只有4个隐层的网络：

  图中是一个四层的全连接网络，假设最简单的情况，激活函数为

，其中i为第i层，x是i层输入，那么

。假设求隐层1的梯度：

，每个函数对于激活函数求导为1，省略了。假设最简单的情况，每个w是一样的，则为w^n-1（n为隐层层数），那么如果w大于1，层数越多，呈指数级爆炸增长，如果w小于1，呈指数级缩小趋近于0。这就是梯度爆炸梯度消失的由来。

2.解决方案

2.1梯度剪切、正则化

梯度剪切是针对梯度爆炸提出的，其思想是设置一个梯度剪切阈值，然后更新梯度的时候，如果超过阈值就将梯度限制为阈值。可以防止梯度爆炸。

2.2使用relu激活函数

  sigmoid求导的曲线如图：

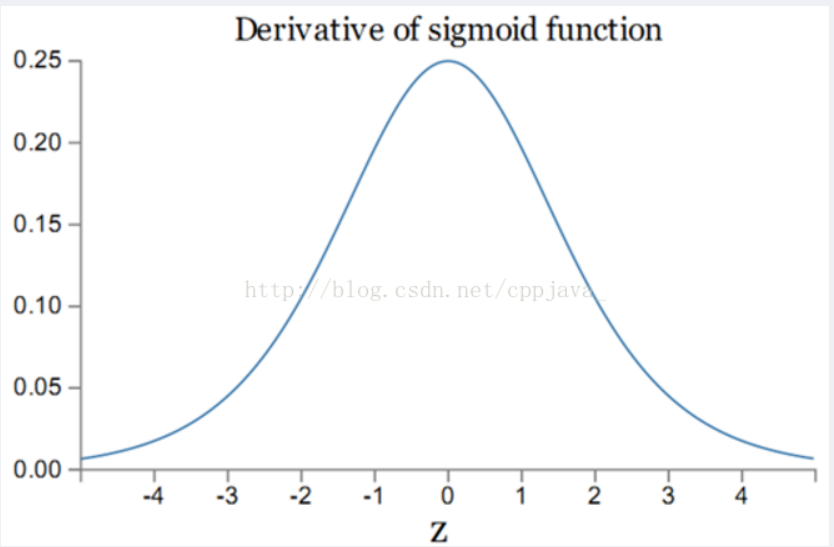
sigmoid的导数最大值为1/4，在求梯度的过程中，很容易出现梯度消失的情况。发生梯度爆炸的情况是w > 4才可能发生。relu可以避免这些。

2.3良好的参数初始化策略也能缓解梯度爆炸问题（权重正则化）

2.4使用残差结构

2.5使用lstm