《Population Based Training of Neural Networks》论文解读

最新推荐文章于 2024-06-06 09:35:06 发布

weixin_33769207

最新推荐文章于 2024-06-06 09:35:06 发布

阅读量676

点赞数

文章标签：人工智能

原文链接：http://www.cnblogs.com/initial-h/p/10519150.html

版权

本文介绍了一种名为PBT(population based training)的异步优化方法，该方法主要用于自适应调节深度学习中的超参数，尤其适用于非静态环境下的深度强化学习。通过种群进化的方式，淘汰差的模型，利用好的模型并添加随机扰动进一步优化，最终得到最优模型。PBT算法在强化学习、监督学习和GAN等多个领域展现出显著效果。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

很早之前看到这篇文章的时候，觉得这篇文章的思想很朴素，没有让人眼前一亮的东西就没有太在意。之后读到很多Multi-Agent或者并行训练的文章，都会提到这个算法，比如第一视角多人游戏(Quake III Arena Capture the Flag)的超人表现，NeurIPS2018首届多智能体竞赛(The NeurIPS 2018 Pommerman Competition)的冠军算法,DeepMind团队ICLR 2019 conference paper的2V2足球,甚至星际争霸II里的AlphaStar，都运用了类似方法。所以这里又回过头记录一下。

文章提出了一种简单的异步优化方法PBT(population based training)，主要用来自适应调节超参数。通常的深度学习，超参数都是凭经验预先设计好的，会花费大量精力且不一定有好的效果，特别是在深度强化学习这种非静态(non-stationary)的环境中，要想得到SOTA效果，超参数还应随着环境变化而自适应调整，比如探索率等等。这种基于种群(population)的进化方式，淘汰差的模型，利用(exploit)好的模型并添加随机扰动(explore)进一步优化，最终得到最优的模型。作者分别从强化学习,监督学习,GAN三个方面做实验，论证了这个简单但有效的算法。
作者认为本文主要做了三点改进:(a)训练过程超参数的自动选择。(b)模型的在线淘汰和选择，让计算资源最大化用在更有希望的模型上(promising models)。(c)超参数在线自适应调节，以适应非静态场景的超参数规划调节(hyperparameter schedules)。

二.效果展示

GAN & RL
左边的gif是GAN在CIFAR-10上的效果，右边是Feudal Networks(FuN)在 Ms Pacman上的效果。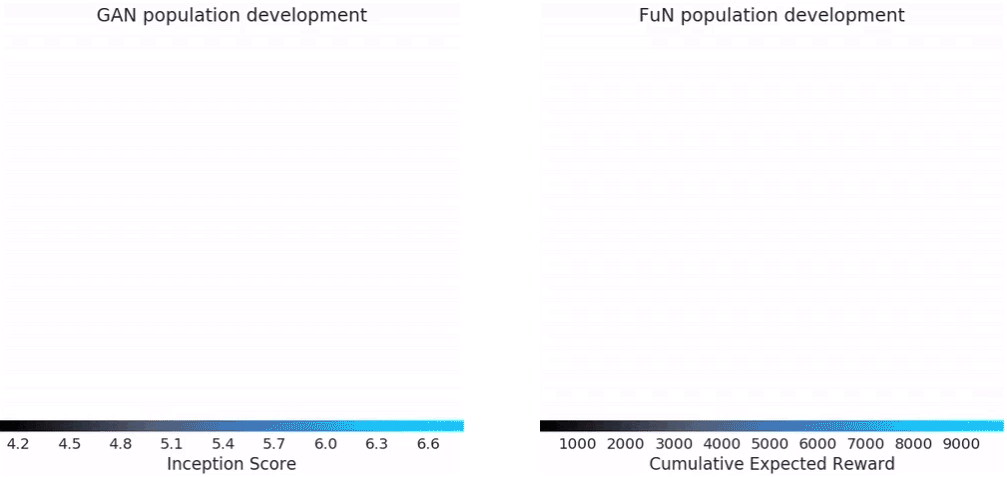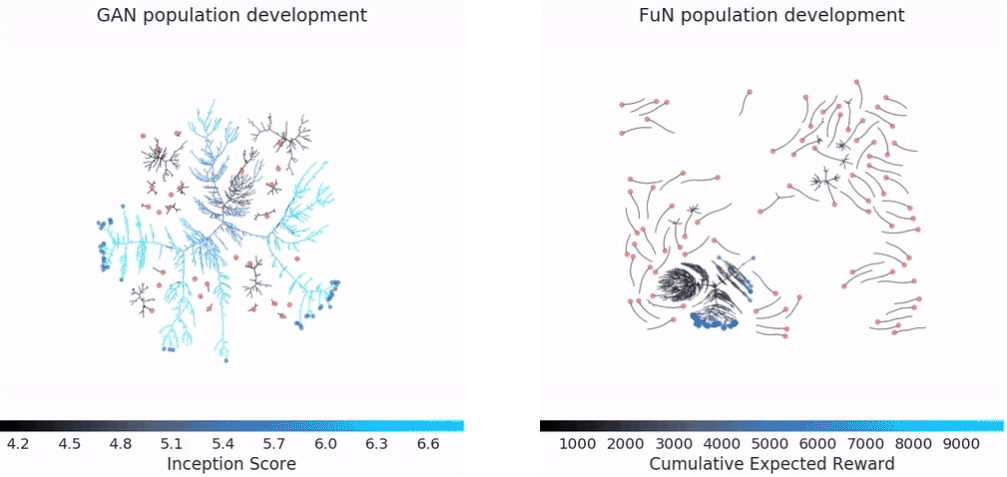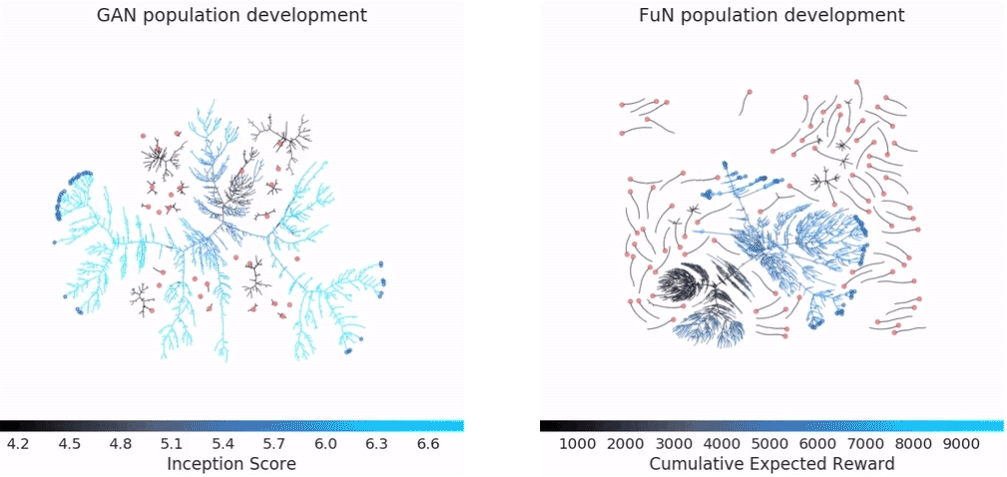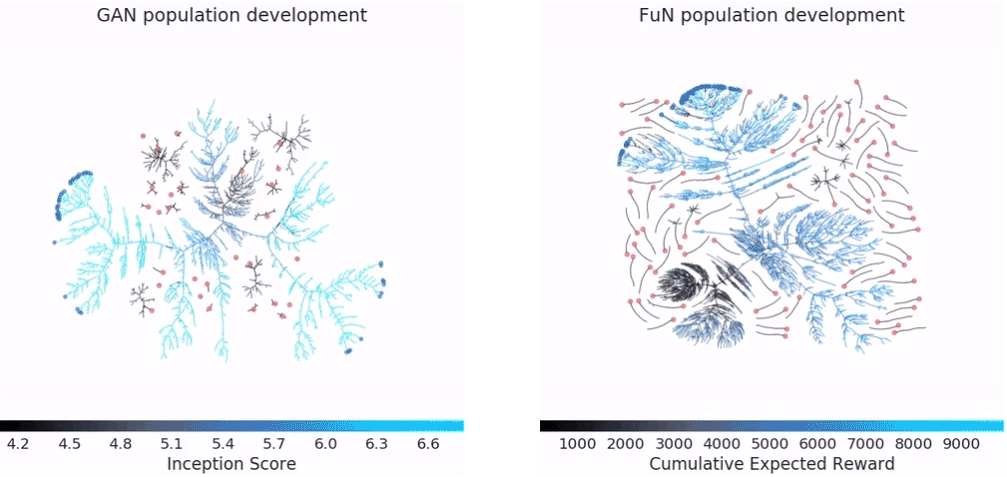

图中红色的点是随机初始化的模型，也就是所谓的population。再往后，黑色的分支就是效果很差的模型，被淘汰掉。蓝色的分支表示效果一直在提升的模型，最终得到的蓝色点就是最优的模型。不得不说，DeepMind这可视化效果做的，真的强。

三.方法细节

问题分析
神经网络的训练受模型结构、数据表征、优化方法等的影响。而每个环节都涉及到很多参数(parameters)和超参数(hyperparameters)，对这些参数的调节决定了模型的最终效果。通常的做法是人工调节，但这种方式费时费力且很难得到最优解。两种常用的自动调参的方式是并行搜索(parallel search)和序列优化(sequential optimisation)。并行搜索就是同时设置多组参数训练，比如网格搜索(grid search)和随机搜索(random search)。序列优化很少用到并行，而是一次次尝试并优化，比如人工调参(hand tuning)和贝叶斯优化(Bayesian optimisation)。并行搜索的缺点在于没有利用相互之间的参数优化信息。而序列优化这种序列化过程显然会耗费大量时间。还有另一个问题是，对于有些超参数，在训练过程中并不是一直不变的。比如监督训练里的学习率，强化学习中的探索度等等。通常的做法是给一个固定的衰减值，而在强化学习这类问题里还会随不同场景做不同调整。这无疑很难找到一个最优的自动调节方式。
具体方法
作者提出了一种很朴素的思想，将并行优化和序列优化相结合。既能并行探索，同时也利用其他更好的参数模型，淘汰掉不好的模型。如图所示，(a)中的序列优化过程只有一个模型在不断优化，消耗大量时间。(b)中的并行搜索可以节省时间，但是相互之间没有任何交互，不利于信息利用。(c)中的PBT算法结合了二者的优点。首先PBT算法随机初始化多个模型，每训练一段时间设置一个检查点(checkpoint)，然后根据其他模型的好坏调整自己的模型。若自己的模型较好，则继续训练。若不好，则替换(exploit)成更好的模型参数，并添加随机扰动(explore)再进行训练。其中checkpoint的设置是人为设置每过多少step之后进行检查。扰动要么在原超参数或者参数上加噪声，要么重新采样获得。作者还写了几个公式来规范说明这个问题，看起来逼格更高一点，我个人觉得没有必要再写在这里了。
伪代码
伪代码非常清楚明白。
其中\(\theta\)表示网络参数，\(h\)表示超参数，\(p\)表示当前模型好坏的指标，\(t\)表示当前第\(t\)代模型（这里说成step应该更准确，多个step之后才生产一代模型，之前理解有点偏差）。整个原理其实和进化算法很像，也和探索利用(exploration vs exploitation)的折中取舍(trade-off)很像。有疑问可以留言交流。

四.实验结果

Toy example
作者举了一个小例子来说明PBT算法的好处，虽然有点牵强，但是也有一定道理。作者假设了一个优化函数：\(Q(\theta)=1.2-(\theta_0^2+\theta_1^2)\)，目标是求该函数的最大值。我们不知道具体函数，只知道该函数的形式是\(\hat{Q}(\theta|h)=1.2-(h_0\theta_0^2+h_1\theta_1^2)\)，其中\(h_0,h_1\)是超参数，\(\theta_0,\theta_1\)是参数。作者对比了PBT，只有替换(exploit)的PBT，只有加随机扰动(explore)的PBT和网格搜索。作者设置了只有两个worker的PBT算法，即初始化两个模型。其中，参数初始化为\(\theta=[0.9,0.9]\)，超参数分别设置为\(h=[1,0]\)和\(h=[0,1]\)。每更新5步设置一个checkpoint。

从上图可以看出，结果显然是PBT效果好。作者举的这个例子比较极端，不过也确实能说明一些道理。就是说在训练过程中超参数也需要不断修正以找到最优值，而PBT算法刚好可以做到这一点。
其他环境效果展示
作者还在一些具体场景上做了实验，比如强化学习，机器翻译，对抗网络等等。这里贴出部分结果，详细参看原文。
- 效果提升展示
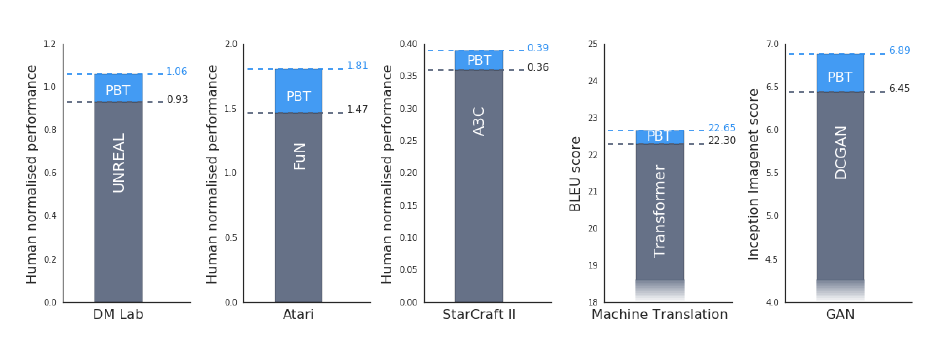
- baseline曲线对比
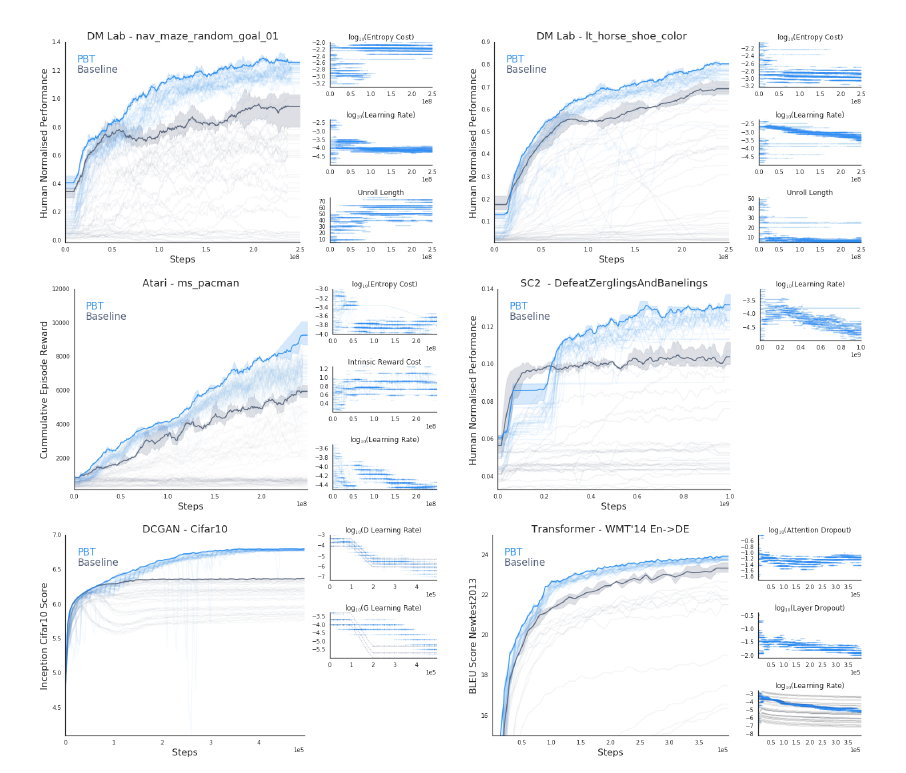
- 对照实验(ablation experiments)