【欧拉回路】【Fleury算法】CDOJ1642 老当益壮，宁移白首之心？

最新推荐文章于 2020-03-07 09:58:54 发布

weixin_33769207

最新推荐文章于 2020-03-07 09:58:54 发布

阅读量107

点赞数

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/autsky-jadek/p/6910405.html

本文介绍如何构造一个特殊的01串，该字符串满足环状且长度为2^n，同时每n位组成的数字都不相同。通过构建欧拉图并使用Fleury算法求解，确保每个点的出入度相等，最终实现无重复遍历。

题意：构造一个01串，使得满足以下条件： 1. 环状（即首尾相连） 2. 每一位取值为0或1 3. 长度是2^n 4. 对于每个(2^n个)位置，从其开始沿逆时针方向的连续的n位01串（包括自己）构成的数均不相同，即0到2^n−1中的数各出现一次数据范围: 1<=n<=15

欧拉回路考虑用一条边表示一个数，那么题目要求就是无重复的遍历完所有边，则这是一个欧拉图的问题。

对于有公共点的两条边，第一个的后n-1位和第二个的前n-1相同。这样将一条边的前n-1位和后n-1位作为点，连边，这样来表示它。如：对于01101，我们可以从0110向1101建一条有向边表示01101. 于是所建图有2^(n-1)个点，和2^n条边。对于任一两个点，如果它们的前n-2位和后n-2位相同，就连一条有向边，这样所得到的图一定是欧拉图，因为每个点的入度和出度都是2，一定存在欧拉回路。

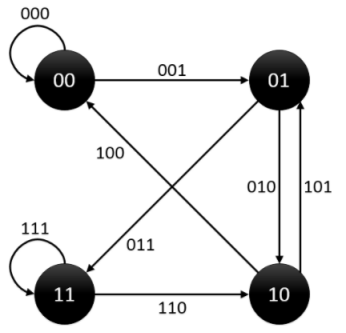
以下代码采取的Fleury算法未经优化，其实应该及时删去已经访问过的边，而非打上标记。这样的复杂度会变高。

#include<cstdio>
using namespace std;
int n;
int v[100010],next[100010],first[20010],e;
void AddEdge(int U,int V){
	v[++e]=V;
	next[e]=first[U];
	first[U]=e;
}
bool vis[100010];
void dfs(int U,bool dep){
	for(int i=first[U];i;i=next[i]){
		if(!vis[i]){
			vis[i]=1;
			dfs(v[i],1);
		}
	}
	if(dep){
		printf("%d",U&1);
	}
}
int main(){
//	freopen("i.in","r",stdin);
	scanf("%d",&n);
	for(int i=0;i<(1<<(n-1));++i){
		AddEdge(i,(i-(i&(1<<(n-2))))<<1);
		AddEdge(i,(i-(i&(1<<(n-2))))<<1|1);
	}
	dfs(0,0);
	puts("");
	return 0;
}

转载于:https://www.cnblogs.com/autsky-jadek/p/6910405.html