在信号处理中常常需要用到曲线拟合,这里介绍一下利用最小二乘拟合一般曲线的方法,并对滤掉信号中白噪声的方法作些介绍。
为了测试拟合算法的好坏,先模拟出一个信号作为检验算法的例子:
- 用白噪声产生模拟信号:
对于理论信号y=y(x),一般可用rand(size(x))和randn(size(x))生成随即噪声信号,两者的区别在于rand生成的噪声信号都是正值,而randn生成的噪声信号则是正负跳跃分布的,所以randn作为白噪声信号,更符合实际情况:
f0=@(c,x)( (x>=0&x<c(1))*0 + (x>=c(1)&x<c(2))*c(3)/(c(2)-c(1)).*(x-c(1)) + (x>=c(2)&x<c(4)).*( (c(5)-c(3))/(c(4)-c(2))*(x-c(2))+c(3) ) + (x>=c(4)&x<c(6))*c(5)/(c(4)-c(6)).*(x-c(6)) + (x>=c(6))*0 );
disp('real c0');
c0=[1, 2, 1, 5, 2, 6]
x_int=0:0.002:10;
y_int=f0(c0,x_int);
%(x_int, y_int) is perfect zigzag signal
%sig=y_int+0.5*rand(size(x_int));
sig=y_int+0.5*randn(size(x_int));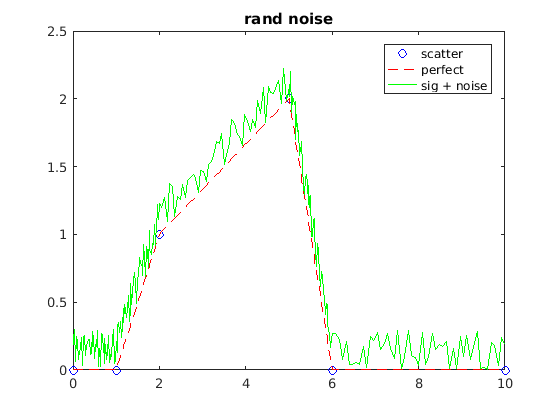





 本文介绍了在信号处理中如何使用Matlab进行最小二乘拟合和滤除白噪声。通过模拟信号,展示了如何利用randn生成白噪声,并通过傅立叶变换进行降噪以提高拟合精度。还提到了Matlab的多项式拟合函数polyfit。
本文介绍了在信号处理中如何使用Matlab进行最小二乘拟合和滤除白噪声。通过模拟信号,展示了如何利用randn生成白噪声,并通过傅立叶变换进行降噪以提高拟合精度。还提到了Matlab的多项式拟合函数polyfit。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 2054
2054

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








