关于树状数组

最新推荐文章于 2025-04-24 15:39:27 发布

转载最新推荐文章于 2025-04-24 15:39:27 发布 · 42 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/xujian9502/archive/2012/01/01/2309396.html

本文详细解释了树状数组的概念及其操作方法，包括插入、建树、求和等关键步骤，并通过实例展示了如何人工模拟实现过程。文章旨在帮助初学者深入理解并掌握树状数组这一数据结构。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

　　刚刚学会树状数组... 开始去网上找相关知识看不懂啊。。。最后自己搞人工模拟终于弄明白了.

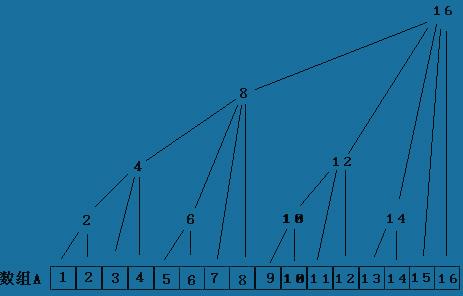
　看上图中下面是数组A 上面是C 注意数组C为标全剩下的元素 C[i]

==A[i].
　　C1 = A1
　　C2 = A1 + A2
　　C3 = A3
　　C4 = A1 + A2 + A3 + A4
　　C5 = A5
　　C6 = A5 + A6
　　C7 = A7
　　C8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8
　　...
　　C16 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8 + A9 + A10 + A11 + A12

+ A13 + A14 + A15 + A16

然后这棵树有这么一个规律.C[i]的管辖范围为2^k(k为把i转化为2进制后末尾的0的个数),且最后一个所管辖的元素必为A[i].. 所以C[i]=A[i+1-2^k]+....+A[i];

　　2^k有这么一个表示方法 i&-i 话说这到底是怎么来的我也不是太清楚。有兴趣可以自己查下有关资料..

1 int lowbit(int a)
2 {
3     return a&(-a);
4 }

　　具体结构就是这样. 然后说一下树状数组的几个操作. 以下介绍中n都为数组A的元素数目。

　　insert 修改数组A中的某一元素. 必然要修改它的父亲就这样不停修改直到把根也改掉.

1 void insert(int temp,int ss) //temp表示当前要修改的节点。ss表示A[i]增加的值 
2 {
3     if(temp>n) //修改完根，退出. 
4         return;
5     c[temp]+=ss; 
6     temp+=lowbit(temp);//temp被赋值为自己的父亲 不懂可以人工模拟下..若不模拟你永远也不懂
7     insert(temp,ss);//修改父亲节点. 
8 }

　　建树操作..就是把A[i]全部插入的过程.

1 void build()
2 {
3     for(int i=1;i<=n;i++)
4         insert(i,a[i]); //注意 建树前C数组赋初值0； 
5 }

　　求前A前i项和很像insert倒过来... 其实这是一个分区求和的过程

1 int getsum(int i)
2 {
3     if(i==0)
4         return 0;
5     int temp;
6     temp=c[i];
7     i-=lowbit(i); //把C[i]所管辖的范围减掉
8     return getsum(i)+temp;    
9 }

　　看不懂的人工模拟其实没几个人能直接看懂的.. 求区间[I,J]的和等于getsum[j]-getsum[i-1].

转载于:https://www.cnblogs.com/xujian9502/archive/2012/01/01/2309396.html