向量几何在游戏编程中的使用系列四之简单的2-D追踪

2019独角兽企业重金招聘Python工程师标准>>>

简单的2-D追踪
　　Andre Lamothe说：“向量几何是游戏程序员最好的朋友”。一点不假，向量几何在游戏编程中的地位不容忽视，因为在游戏程序员的眼中，显示屏幕就是一个坐标系，运动物体的轨迹就是物体在这个坐标系曲线运动结果，而描述这些曲线运动的，就是向量。使用向量可以很好的模拟物理现象以及基本的AI.
　　现在，先来点轻松的，复习一下中学知识。
　　向量v(用粗体字母表示向量)也叫矢量，是一个有大小有方向的量。长度为1的向量称为单位向量，也叫幺矢，这里记为E.长度为0的向量叫做零向量，记为0，零向量没有确定方向，换句话说，它的方向是任意的。
　　一、向量的基本运算

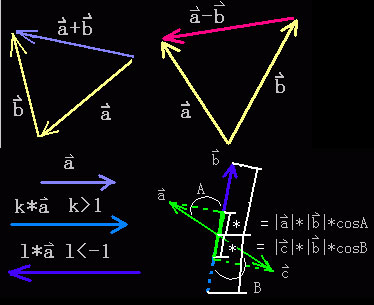
　　1、向量加法：a+b等于使b的始点与a的终点重合时，以a的始点为始点，以b的终点为终点的向量。
　　2、向量减法：a-b等于使b的始点与a的始点重合时，以b的终点为始点，以a的终点为终点的向量。
　　3、 数量乘向量：k*a，k>0时，等于a的长度扩大k倍；k=0时，等于0向量；k<0时，等于a的长度扩大|k|倍然后反向。
　　4、向量的内积(数量积、点积)： a.b=|a|*|b|*cosA 等于向量a的长度乘上b的长度再乘上a与b之间夹角的余弦。
　　它的几何意义就是a的长度与b在a上的投影长度的乘积，或者是b的长度与a在b上投影长的乘积，它是一个标量，而
　　且可正可负。因此互相垂直的向量的内积为0.

                    

　　5、向量的矢积(叉积)： a x b = |a|*|b|*sinA*v = c， |a|是a的长度，|b|是b的长度，A是a和b之间的锐夹角，v是与a，b所决定的平面垂直的幺矢，即axb与a、b都垂直。a，b，c构成右手系，即右手拇指伸直，其余四指按由a到b的锐角蜷曲，此时拇指所指方向就是c的方向。因此axb！=bxa，bxa是手指朝b到a的锐角蜷曲时，拇指指向的方向，它和c相反，即-c.a x b的行列式计算公式在左右手坐标系下是不同的，如上图所示。两个向量的矢积是一个向量。
　　6、正交向量的内积：互相垂直的两个向量是正交的，正交向量的内积为零。a.b = |a|.|b|*cos(PI/2) = |a|.|b|*0 = 0.
　　二、向量的性质
　　没有下面的这些性质做基础，我们后面向量技巧的推导将无法进行。
　　1) a + b = b + a
　　2) (a + b) + c = a + (b + c)
　　3) a + 0 = 0 + a = a
　　4) a + (-a) = 0
　　5) k*(l*a) = (k*l)*a = a*(k*l)
　　6) k*(a + b) = k*a + k*b
　　7) (k + l)*a = k*a + l*a
　　8) 1*a = a
　　9) a.b = b.a
　　10)a.(b + c) = a.b + a.c
　　11)k*(a.b) = (k*a)。b = a.(k*b)
　　12)0.a = 0
　　13)a.a = |a|^2
　　三、自由向量的代数(分量)表示
　　1、向量在直角坐标中的代数表示方法：
　　a=(x，y)
　　其中x，y分别是向量在x轴和y轴上的分量。任何一个在直角坐标轴上的分量为(x，y)的向量都相等。比如上图中的每个向量都表示为(-2，1)。
　　或者写成a=x*i+y*j，即i和j的线性组合，这里i是x轴方向的单位向量(1，0)，j是y轴方向的单位向量(0，1)，因此i正交于j.任意一个2-D向量都可以表成i与j的线性组合。
　　|i| = |j| = 1

转载于:https://my.oschina.net/liu-xuewei/blog/77399