红黑树
红黑树的性质:
- 性质 1：每个节点要么是红色，要么是黑色。
- 性质 2：根节点永远是黑色的。
- 性质 3：所有的叶节点都是空节点（即 null），并且是黑色的。
- 性质 4：每个红色节点的两个子节点都是黑色。（从每个叶子到根的路径上不会有两个连续的红色节点）
- 性质 5：从任一节点到其子树中每个叶子节点的路径都包含相同数量的黑色节点。
红黑树的高度:
black-height--红黑树从根节点到每个叶子节点的路径都包含相同数量的黑色节点，因此从根节点到叶子节点的路径中包含的黑色节点数被称为树的“黑色高度（black-height.
插入操作:
由于红黑树只是一个特殊的排序二叉树，红黑树的插入删除和排序二叉树相同,只是影响了平衡性能,因此需要插入和删除后修复.
插入修复:
添加节点后修复:(有以下可知,基本上需要关心的是3,4,这是因为加如的新节点为红色,不能连续出现两个红色节点,破环了性质4,因此我们需要修复的是不满足性质(4) (u-uncle;p-parent;g-grandparent为下面用到的简写)
- 新节点 N 是树的根节点，没有父节点---只需把此节点设置位黑色即可
- 新节点的父节点 P 是黑色--无需操作
- 父节点是祖父节点的左孩子且父节点为红色--此时,不管新加入的节点时左孩子还是右孩子,明显左边过长,需要右旋.
- 叔叔节点是红色--------u,p变为黑色,g变为红色,且继续检测g以上的节点是否满足,可能导致g颜色的变化引起上面节点不满足性质4,故需要将g设为新的变化节点,继续忘上进行调整.
- 叔叔是黑色，且当前节点是右孩子---先左旋p,得到下面的情况,防止直接旋转得到右边过长.
- 叔叔是黑色，且当前节点是左孩子。--将p设为黑色,将G设为红色,右旋.---此时,其父节点为黑色,循环停止
- 父节点是祖父节点的左孩子且父节点为红色--此时,不管新加入的节点时左孩子还是右孩子,明显左边过长,需要左旋.
- 叔叔节点是红色-------u,p变为黑色,g变为红色,且继续检测g以上的节点是否满足,可能导致g颜色的变化引起上面节点不满足性质4,故需要将g设为新的变化节点,继续忘上进行调整.
- 叔叔是黑色，且当前节点是左孩子---先右旋,得到下面的情况,防止直接旋转导致左边过长
- 叔叔是黑色，且当前节点是右孩子。--将p设为黑色,将G设为红色,左旋.---此时,其父节点为黑色,循环停止.
插入及其修复代码:
public void insert(Node node) {
node.color = RED;
Node cur = mroot;
Node tmp = null;
int num;
//找到要插入的父节点
while (cur != null) {
tmp = cur;
num = cmp.compare(tmp, node);
cur = num > 0 ? tmp.left : tmp.right;
}
node.parent = tmp;
if (tmp != null) {
num = cmp.compare(tmp, node);
if (num >= 0) {
tmp.left = node;
} else {
tmp.right = node;
}
} else {
mroot = node;
}
fixInsertRBT(node);
}
private void fixInsertRBT(Node node) {
Node p, g, u;
//情况3,4
while (node.parent != null && node.parent.color == RED) {
p = node.parent;
g = p.parent;
//情况3:p为g的左孩子
if (p == g.left) {
//g必定不会为空当没有祖父节点的时候就不会跳进此循环
u = g.getRight();
//如果p,u都为红色.
if (u != null && u.color == RED) {
p.color = BLACK;
u.color = BLACK;
g.color = RED;
node = g;
} else {
//当node为右孩子的时候,先左旋,使得不至于直接旋转导致右边过长,从而造成不平衡.
if (node == p.right) {
rotateLeft(p);
Node tmp = p;
p = node;
node = tmp;
}
//当node 为左孩子的时候
p.color = BLACK;
g.color = RED;
rotateRight(g);
}
}
//情况4--p为g的右孩子
else {
u = g.getLeft();
if (u != null && u.color == RED) {
p.setColor(BLACK);
u.setColor(BLACK);
g.setColor(RED);
node = g;
} else {
if (node == p.left) {
rotateRight(p);
Node tmp = p;
p = node;
node = tmp;
}
//当node 为左孩子的时候
p.color = BLACK;
g.color = RED;
rotateLeft(g);
}
}
}
//满足情况1,实际上增加黑色节点高度必定时从这里修改的,因为下面为了保持性质5黑色节点高度
// 不会增加,但是当新增节点最后导致根节点变为了红色,此时就会增加红黑树黑色节点高度.
mroot.setColor(BLACK);
}
左旋及右旋的代码:
void rotateLeft(Node data) {
Node temp = data.right;
data.right = temp.left;
if (data.right != null) {
data.right.parent = data;
}
temp.parent = data.parent;
if (data.parent == null) {
mroot = temp;
} else if (data.parent.left == data) {
temp.parent.left = temp;
} else {
temp.parent.right = temp;
}
temp.left = data;
data.parent = temp;
}
void rotateRight(Node data) {
Node temp = data.left;
data.left = temp.right;
if (data.left != null) {
data.left.parent = data;
}
//交换父节点
if (data.parent == null) {
mroot = temp;
} else if (data.parent.left == data) {
data.parent.left = temp;
} else {
data.parent.right = temp;
}
temp.parent = data.parent;
temp.right = data;
data.parent = temp;
}
具体演化过程见我手画的图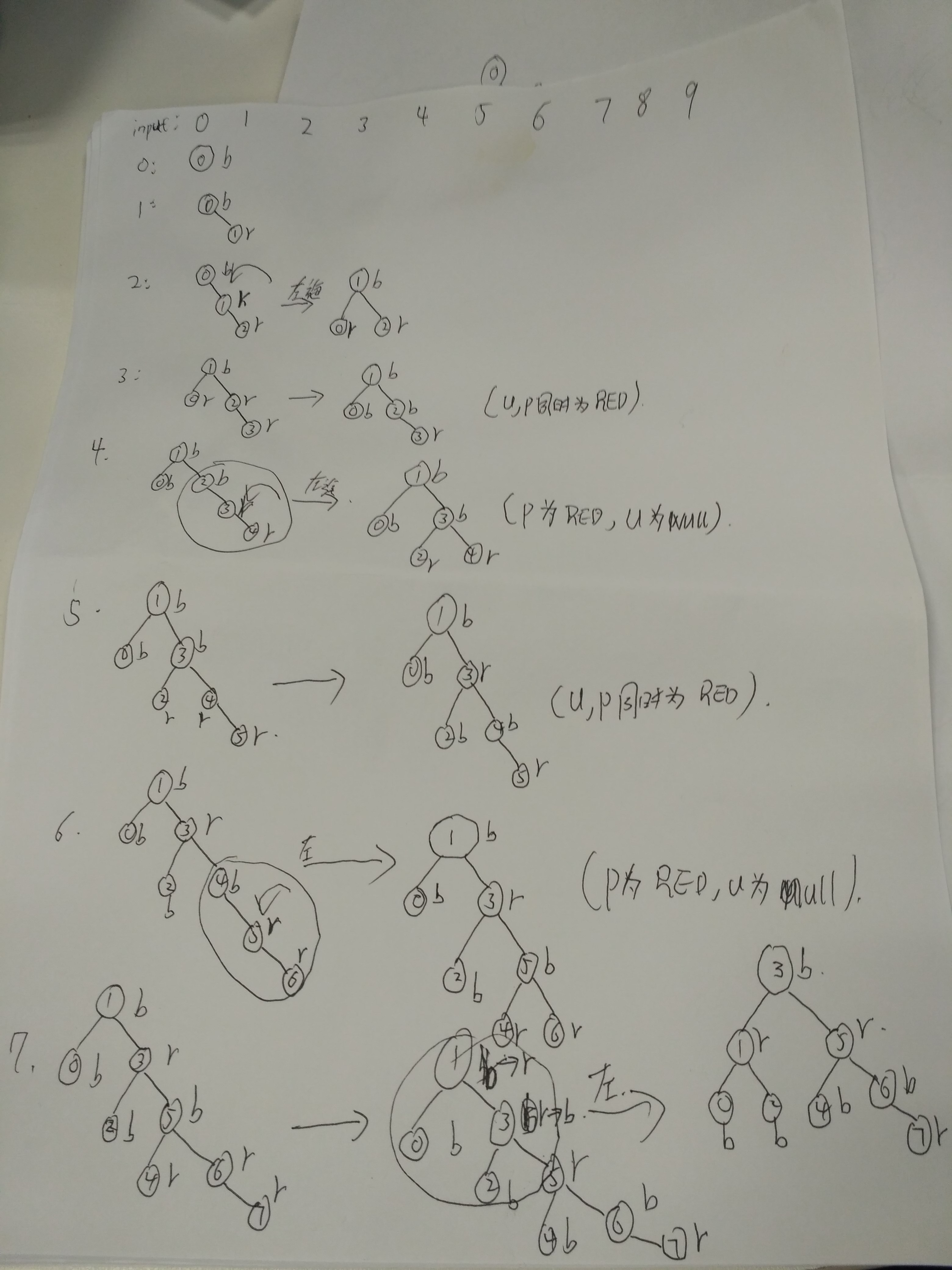 
求后继节点:
求p节点后继节点:分为2种情况
- p节点有右子树--则其后继节点为其右子树的最小节点(这个会在节点删除的时候被调用)
- p节点没有右子树--分为两种情况
- p节点的父节点及其祖父节点依次循环大于其父节点,即(p.parent.key>p.parent.parent.key),此种情况导致p没有后继节点,因为p是最大的那个节点
p.parent=p.parent.parent,依次找到其父节点们第一个为左子树的情况,则此祖父节点为p的后继节点.
Node successor(Node data) {
if (data == null) {
return null;
}
//后继节点是右节点为根的整棵树上的最小节点
else if (data.right != null) {
return findMinNode(data.right);
}
//如果没有右节点,则必为其第一颗为左子树的祖父(包括父亲)节点(因为其祖父类节点若为右子树,
// 必定小于其前一个祖父类节点,一次类推,需要第一颗左子树祖父类节点,若一直到头没有,则说明
// 删除的是整个树的最大节点,故后继节点为null)
else {
Node s = data.parent;
Node tmp = data;
while (s != null && tmp == s.right) {
tmp = s;
s = s.parent;
}
return s;
}
}
Node findMinNode(Node root) {
if (root == null) {
return null;
} else {
Node min = root;
while (min.left != null) {
min = min.left;
}
return min;
}
}
删除节点
删除节点分为4大类:
- 被删除节点只有左子树--则用其右孩子代替其位置
- 被删除节点只有左孩子--则用其左孩子代替其位置
- 被删除节点既有左孩子又有右孩子--则把其后继节点的值copy过来,其后继节点必定没有左孩子,并把后继节点代替其为被删除节点(值已经被copy了,所以可以删除后继节点),其后继节点或者只有左孩子,变为情况2,或者没有孩子,变为情况4
- 被删除节点没有孩子--分为两大类
- 被删除节点为根节点则此树被全部删除
- 被删除节点为叶子节点则删除即可.
String remove(int key) {
Node node = getNode(key);
if (node == null) {
return null;
}
String oldValue = node.value;
remove(node);
// deleteNode(node);
return oldValue;
}
private void remove(Node node) {
Node p = node;
//将被删除的节点改为删除其后继节点,并把后继节点的值copy过来
if (node.left != null && node.right != null) {
Node s = successor(node);
p.key = s.key;
p.value = s.value;
p = s;
}
//replacement有4中情况得来,(1)只有左孩子(2)只有右孩子
//(3)左孩子右孩子都不为空时其后继节点的左孩子必为空.
//(4)为空,又分为两种情况:一是被删除的节点是唯一一个节点,二是被删除的节点是叶子节点.
Node replacement = (p.left == null ? p.right : p.left);
if (replacement != null) {
replacement.parent = p.parent;
//删除的是跟节点
if (p.parent == null) {
mroot = replacement;
} else if (p.parent.left == p) {
p.parent.left = replacement;
} else {
p.parent.right = replacement;
}
p.left = p.right = p.parent = null;
if (p.color == BLACK) {
//
fixDeletionRBT(replacement);
}
}
//单独的一个节点
else if (p.parent == null) {
mroot = null;
}
//叶子节点
else {
if (p.parent.left == p) {
p.parent.left = null;
} else {
p.parent.right = null;
}
p.parent = null;
if (p.color == BLACK) {
//
fixDeletionRBT(p);
}
}
}
测试:懒得没有写全,基本上人工看了一下.
@Test
public void remove() throws Exception {
Node node8 = new Node(8, "8");
Node node4 = new Node(4, "4");
Node node12 = new Node(12, "12");
Node node2 = new Node(2, "2");
Node node6 = new Node(6, "6");
Node node10 = new Node(10, "10");
Node node14 = new Node(14, "14");
Node node1 = new Node(1, "1");
Node node3 = new Node(3, "3");
Node node5 = new Node(5, "5");
Node node7 = new Node(7, "7");
Node node9 = new Node(9, "9");
Node node11 = new Node(11, "11");
Node node13 = new Node(13, "13");
Node node15 = new Node(15, "15");
keyStore.insert(node8);
keyStore.insert(node4);
keyStore.insert(node12);
keyStore.insert(node2);
keyStore.insert(node6);
keyStore.insert(node10);
keyStore.insert(node14);
keyStore.insert(node1);
keyStore.insert(node3);
keyStore.insert(node5);
keyStore.insert(node7);
keyStore.insert(node9);
keyStore.insert(node11);
keyStore.insert(node13);
keyStore.insert(node15);
//测试删除根节点-----相当于既有left,又有right
keyStore.levelScan();
keyStore.remove(8);
System.out.println("删除节点以后");
keyStore.levelScan();
//测试删除节点只有右子树
keyStore.remove(10);
System.out.println("删除节点以后");
keyStore.levelScan();
//测试删除叶子节点
keyStore.remove(15);
System.out.println("删除节点以后");
keyStore.levelScan();
//测试删除节点只有左子树
keyStore.remove(14);
System.out.println("删除节点以后");
keyStore.levelScan();
//测试删除叶子节点
keyStore.remove(3);
keyStore.levelScan();
keyStore.removeAll();
keyStore.insert(new Node(1,"1"));
//删除单节点
keyStore.remove(1);
keyStore.levelScan();
}
删除节点后修复:
-
分析上面我们删除的那个非叶子节点的情况,删除p后,当p为黑色,造成了p以下的树的黑色高度少1(违反性质5),故需要修复.那么我画图分析:
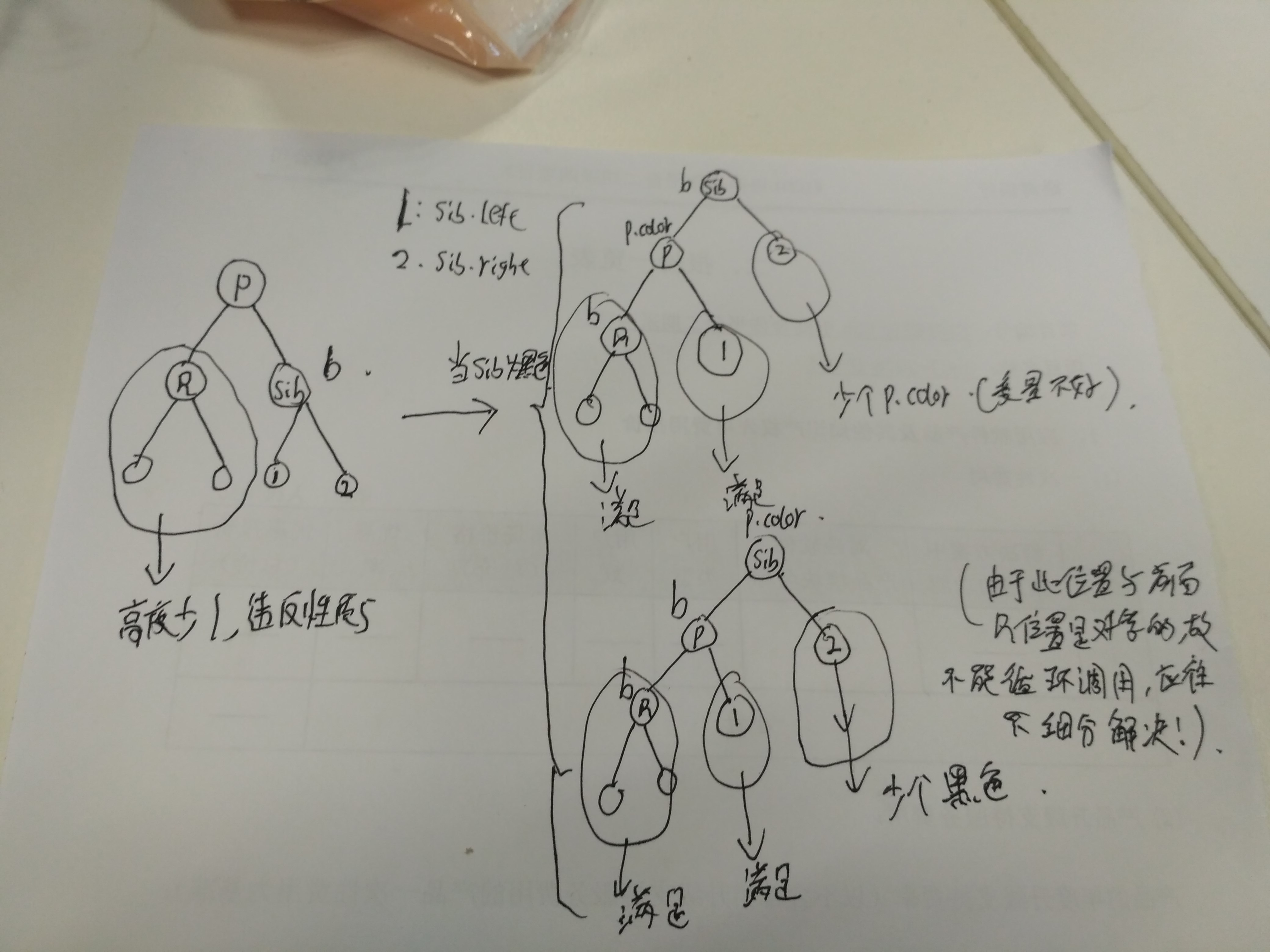上图中,我分析了当R是左子树的情况(当右子树的时候对称):分为以下几种情况:-
当
R.color==RED时,我们直接将R.color=BLACK则问题解决. -
当
R.color=BLACK时,我们采用变换为右侧下面的方案.这样就只用解决这边少个黑色的问题了.- 由于我们需要让R这边的路径上多个黑色节点,因此我们有限考虑简单的情况,当
sib.color==BLACK时,我们通过以下变换得到右边下面得变换.
- 由于我们需要让R这边的路径上多个黑色节点,因此我们有限考虑简单的情况,当
sib.color=p.color; p.color=BLACK; rotateLeft(p); ``` 此时,我们解决新的2节点路径少1问题. 1. 当`2.color==RED`得话,我们让`2.color=BLACK`就解决了. 2. 当`2.color==BLACK` - 当 `1.color==RED`得时候,我们希望通过变换得到2这个位置得颜色为红色解决.,故右旋可以得到.  代码: ```java sib.left.color=BLACK; sib.color=RED; rotateRight(sib); ``` 然后,此问题变为了上面得1.,被解决. - 当 `2.color==BLACK`的时候,这时候,sib及其子节点都是黑色,我们发现不好再旋转了,此时,我们把sib的颜色变为红色,相当于sib及其子节点也黑色路径少1,于是变为整个p的路径少1,此时p相当于前面的R节点,于是我们把问题又往上递归了一层.此时又分为两种情况:1是问题又变为了R,R的其他情况我们能够解决,当时如果再继续网上推到父节点呢?我们假设一直推到根节点的左子树,我们继续推到根节点以下的路径都少1,我们发现,此时整个树自动平衡了,整个树的长度少了1.故而此种循环是可以的. 3. 当`sib.color==RED`时(p必为黑色),我们不希望再分了,我们希望把它通过旋转变为黑色的节点,然后调用上面的解法就OK了.  通过上图我们发现我们变换后和变换前各节点高度没有发生变化,此时我们将节点1设为新的sib节点,且节点1必为黑色,从而达到了我们的目的. 代码: ```java p.color=RED; sib.color=BLACK; rotateLeft(p); sib=p.right; ``` 至此,非叶子节点的删除我们分析完了. 下面我们分析叶子节点的删除:当被删除的叶子节点为黑色节点时,可能违反性质5,导致该路径长度少1.由于此节点一旦删除,修复函数需要传如=入一个参数,没办法传,所以先修复,让此路径长度多1,再删除此节点,则全树平衡. - 此节点不是原来被删除节点的位置,时某后继节点,从而是个左子树. - 此节点直接就是原来被删除节点,时最大值,没有后继节点. ,我们发现,情况和非叶子节点变成了一样.故而,我们看作一种情况处理,但不同的是,非叶子节点是路径先缺少了1,我们才修复后平衡,而叶子节点是我们先修复让此路径长度多1,后删除达到平衡! 3. 当`sib.color==RED`时(p必为黑色),我们不希望再分了,我们希望把它通过旋转变为黑色的节点,然后调用上面的解法就OK了. ```Java private void fixDeletion(Node node) { while (node.color == BLACK && node != mroot) { //左子树 if (node == node.parent.left) { Node bro = node.parent.right; //把兄弟节点为红色的情况经过旋转统一为兄弟节点为黑色的情况处理. if (bro.color == RED) { bro.color = BLACK; node.parent.color = RED; rotateLeft(node.parent); bro = node.parent.right; } if (hasTwoChild(bro)) { bro.color = RED; node = node.parent; } else { if (bro.right.color == BLACK) { bro.left.color = BLACK; bro.color = RED; rotateRight(bro); bro = node.parent.right; } bro.color = node.parent.color; node.parent.color = BLACK; bro.right.color = RED; rotateLeft(node.parent); node = mroot; } } //右子树 else { Node bro = node.parent.left; //当bro.color==RED,转换为黑色,则node.parent.color==bro.left.color==bro.right.color==BLACK if (bro != null && bro.color == RED) { bro.color = BLACK; node.parent.color = RED; rotateRight(node.parent); bro = node.parent.left; } if (hasTwoChild(bro)) { assert bro != null; bro.color = RED; node = node.parent; } else { assert bro != null; if (bro.left.color == BLACK) { bro.right.color = BLACK; bro.color = RED; rotateRight(bro); bro = node.parent.left; } //当bro.left.color==RED&&bro.color==BLACK bro.color = node.parent.color; node.parent.color = BLACK; rotateRight(node.parent); bro.left.color = BLACK; node = mroot; } } } node.color = BLACK; } -
测试
@Test
public void fixDeletion() throws Exception {
for (int i = 1; i <= 18; i++) {
keyStore.insert(new Node(i, i + ""));
}
keyStore.levelScan();
keyStore.remove(17);//只需将节点18替补上来变为黑色.
Node node = keyStore.getMroot().right.right.right.right;
assertThat(node.getValue(), is("18"));//右节点补位
assertThat(node.color, is(BLACK));
System.out.println(keyStore.remove(5));
System.out.println("删除5后");
keyStore.levelScan();
}
- 问题,为啥我写的红黑书bro.left和bro.right存在空指针问题,而TreeMap不存在这个问题.这个还需要研究一下! 搞明白了,我就说它怎么这么神,没有空指针问题,原因是这个!
private static <K, V> boolean colorOf(Entry<K, V> p) {
return (p == null ? BLACK : p.color);
}
扫一扫
648
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
