拓展

2019独角兽企业重金招聘Python工程师标准>>>

• 时间段变化的泊松回归

假设结果变量是一个比率。为分析比率，必须包含一个记录每个观测的时间长度的变量（如time）。然后，将模型从

 

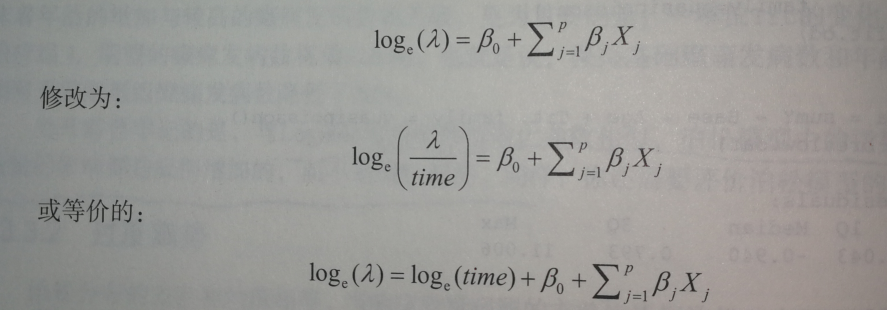
为拟合新的模型，需要设置glm()函数中的offset选项，例如在Breslow癫痫研究中，假设病人随机分组后的检测时间长度挺在14到60天间变化。你可以将癫痫发病率作为因变量（假设已记录了每个发病的时间），然后拟合模型：

fit.od <- glm(sumY ~ Base + Age + Trt, data=breslow.dat,
              offset=log(time),family=poisson())   #增加了offset=log(time)

其中sumY指随机化分组后在每个病人被研究期间其癫痫发病的次数，此处假定比率不随事件变化（比如，4天中发生2次癫痫与20天发生10次癫痫比率相同）

• 零膨胀泊松回归
• 结果零值

以Logistic回顾回归中的婚外情为例，初始结果变量（affairs）记录了调查对象婚外情的次数，有些调查者从不婚外情，结构为0，这便称为结构零值

此时可以使用 零膨胀泊松回归

pscl包中的zeroinfl()函数可做零膨胀回归，该模型相当于Logistic回归(预测结构零值)和泊松回归（预测无结构零值观测的计数）的组合

• 稳健泊松回归

robust包中的glmRob()函数可以拟合稳健广义线性模型那个，包含稳健泊松回归，当存在离群点和强影响点时用该方法很有效

 

转载于:https://my.oschina.net/u/1785519/blog/1563554