[Leetcode] Longest Palindromic Substring

最新推荐文章于 2025-08-22 01:16:35 发布

转载最新推荐文章于 2025-08-22 01:16:35 发布 · 56 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/seagoo/p/5000564.html

文章标签：

#数据结构与算法 #java

本文介绍了一种通过动态规划方法寻找字符串中最长回文子串的算法。使用布尔矩阵记录子串是否为回文，并逐步扩大子串范围，最终找到最长的回文子串。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

问题：

Given a string S, find the longest palindromic substring in S. You may assume that the maximum length of S is 1000, and there exists one unique longest palindromic substring.

假设 f(i, j) 表示字符串S中下标从i到j的子串是否为回文，其值为true或false，那么用如下的公式来递归计算所有i，j组合的f(i, j):

我们只考虑i <= j 的情形
如果i == j, 那么 f(i, j) 表示S中只包含一个字符的子串是否为回文，这个子串肯定是回文，因此 f(i, j) = true;
如果i + 1 = j, 那么 f(i, j) 表示S中只包含前后相邻的两个字符的子串是否为回文，因此其值又这两个字符是否相等决定，即 f(i, j) = S.charAt(i) == S.charAt(j).
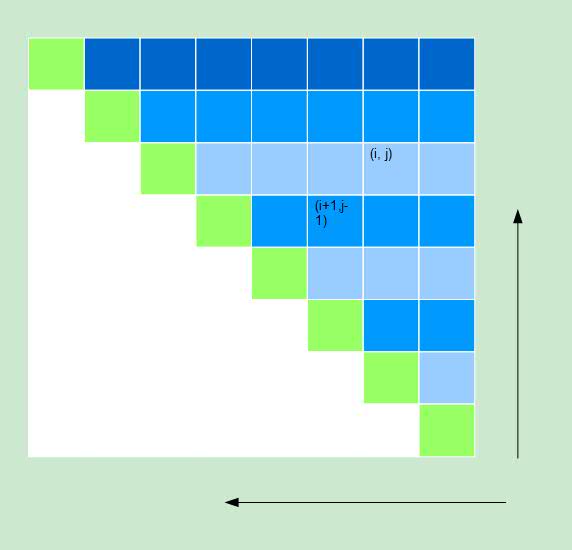
如果i + 1 < j, 那么 f(i, j) 表示S中至少包含三个字符的子串是否为回文，这时如果i处的字符等于j处的，并且夹在它们之间的子串也是回文的话，那么该子串就也是回文，否则就不是。因此，
f(i, j) = S.charAt(i) == S.charAt(j) && f(i + 1, j - 1).

总结一下，
当i == j时，f(i, j) = true
当i + 1 = j时，f(i, j) = S.charAt(i) == S.charAt(j)
当i + 1 < j时，f(i, j) = S.charAt(i) == S.charAt(j) && f(i + 1, j - 1)

根据这个公式，计算所有f(i, j)并在计算过程中记录最长子串的长度和起始位置。

Java代码如下：

 1 public class Solution {
 2     public String longestPalindrome(String s) {
 3         boolean[][] maxtrix = new boolean[s.length()][];
 4         int start = 0, end = -1, longest = 0;
 5         for(int i = s.length() -1; i >= 0; i--) {
 6             maxtrix[i] = new boolean[s.length()];
 7             for(int j = s.length() - 1; j >= i; j--) {
 8                 if(j - i == 0) {
 9                     maxtrix[i][j] = true;
10                 }else if(j - i == 1) {
11                     maxtrix[i][j] = s.charAt(i) == s.charAt(j);
12                 }else {
13                     maxtrix[i][j] = s.charAt(i) == s.charAt(j) && maxtrix[i + 1][j - 1];
14                 }
15                 if(j - i + 1 > longest && maxtrix[i][j]) {
16                     longest = j - i + 1;
17                     start = i;
18                     end = j;
19                 }
20             }
21         }
22         return s.substring(start, end + 1);
23     }
24 }