第三期 行为规划——8.速度惩罚的代价函数

在我们想要的时候获得转换的关键部分，他们要设计合理的成本函数。

我们想惩罚和奖励正确的事情。我将通过一个例子来说明，您可能会考虑设计成本函数的一种方法。

我们来考虑如何设计车速的成本函数。一方面，我们想快速到达目的地，但另一方面，我们不想违法。

我们必须控制的基本数量是汽车所需的速度。有些速度更有高效，有些甚至是非法的。

让我们填入这张图，并尝试为每个速度分配一些成本。

为了简单起见，让我们假设所有的成本函数都会有一个0到1之间的输出。

稍后我们将通过调整权重来调整每个成本函数的重要性。

假设我们所在的道路限速在这里。那么，我们知道如果我们的速度超过限速，

这应该是最大的成本。也许我们想要设置，这是一个理想的零成本速度，稍低于速度限制，以便我们有一些缓冲区。

然后我们可以考虑我们要惩罚多少停车。显然，停车是坏事，但也许不如打破速度限制那样糟糕，所以我们会把它放在这里。

为了简单起见，我们可以说零和目标速度之间存在线性成本。

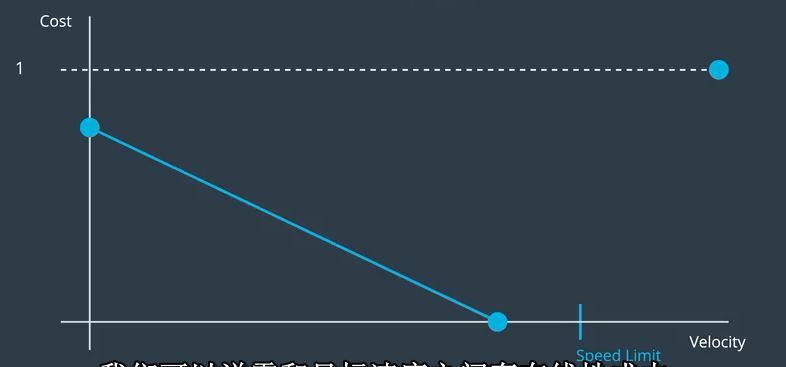
而且由于违法是一件二元的事情，我们只要说任何速度大于或等于速度极限具有最大成本。再次，我们可以随意将这些点连接起来

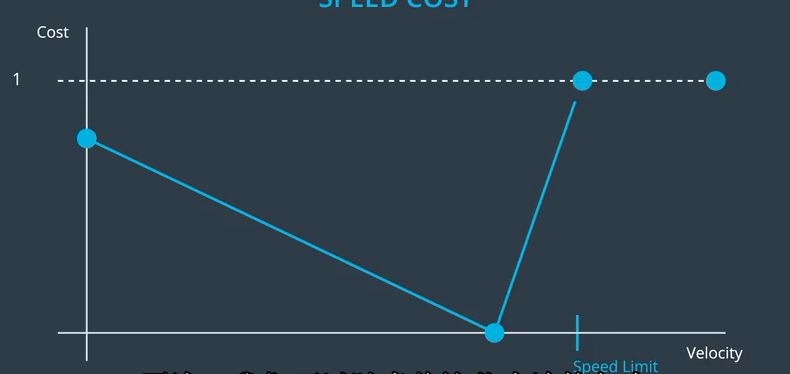
线性函数和超出限制速度的平面最大成本。现在，在实践中，我们可能实际上想要参数化一些

这些数量以便我们稍后可以调整它们直到我们得到正确的行为。所以首先，我们可以定义一个名为Stop Cost for的参数

零速度情况和被调用的参数缓冲速度可能是每小时几英里。

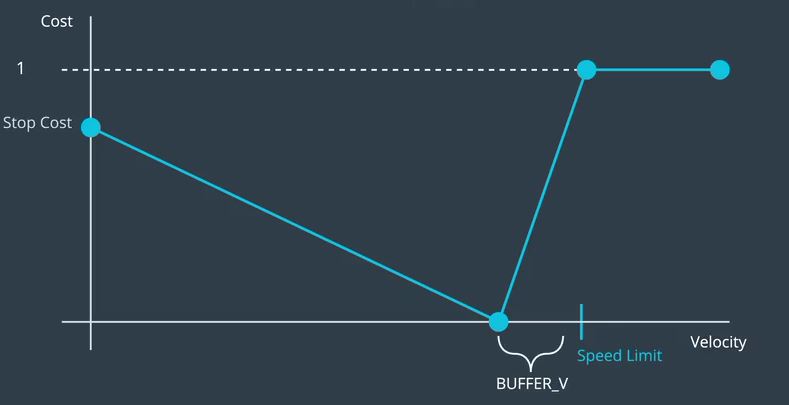
那么，我们的总体成本函数有三个领域。如果我们低于目标速度，成本函数看起来像这样。

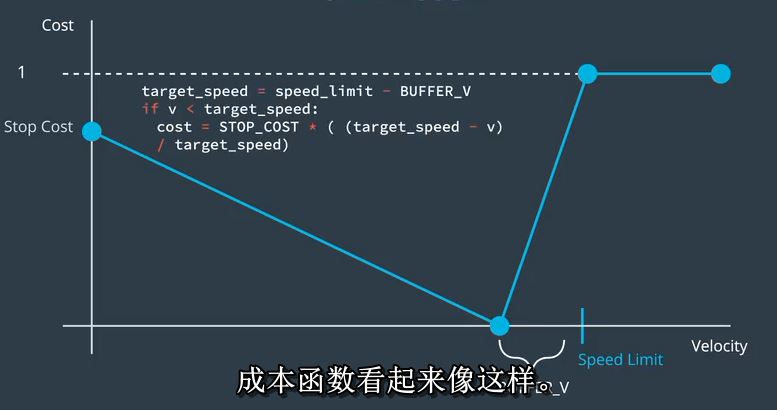
如果我们超过限速，成本只是一个。

如果我们之间，成本看起来像这样。真棒。

 

转载于:https://www.cnblogs.com/fuhang/p/8995233.html