1. 球面余弦定律
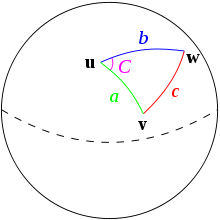
http://wenku.baidu.com/view/52278c3943323968011c92dc.html 证明。
http://en.wikipedia.org/wiki/Spherical_law_of_cosines
2.大圆距离
http://en.wikipedia.org/wiki/Great-circle_distance
方法1:

证明:
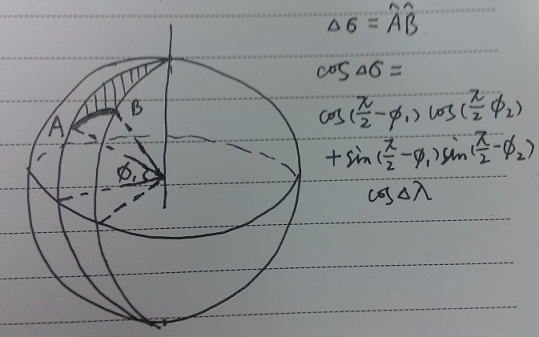
方法2:

3.椭圆上两点间距离——大地线,大地主题解算
1. 球面余弦定律

http://wenku.baidu.com/view/52278c3943323968011c92dc.html 证明。
http://en.wikipedia.org/wiki/Spherical_law_of_cosines
2.大圆距离
http://en.wikipedia.org/wiki/Great-circle_distance
方法1:

证明:

方法2:

3.椭圆上两点间距离——大地线,大地主题解算
 928
928

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


