神经网络中的反向传播算法

最新推荐文章于 2025-08-11 16:25:07 发布

转载最新推荐文章于 2025-08-11 16:25:07 发布 · 112 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：https://my.oschina.net/lvyi/blog/620845

文章标签：

#人工智能 #php #数据结构与算法

为什么80%的码农都做不了架构师？>>>

「概率论与数理统计」中的随机变量及其分布中，会使用正态分布，二值分布等等去套这些变量数据，最后去估计确定这些分布中的参数。

在机器学习中，线性回归和逻辑回归也都是先选择一个数据模型，然后使用一定的方法去确定模型的参数。最基本的方法就是代价函数。代价函数评价假设函数 h 和真实函数 f （这个函数未知）之间的差异，当两者相差不大时，即可以用假设函数 h 代替真实函数 f。

梯度下降算法只是代价函数的优化算法，加速了参数的求解过程。

在神经网络中，同样使用梯度下将算法来求解参数。同样，梯度下降也有优化，这就是反向传播算法。反向传播算法加速了梯度下降中的偏导求解。

BP 网络函数逼近实例

% 1.首先定义正弦函数，采样率为20Hz，频率为1Hz
k = 1; % 设定正弦信号频率
p = [0:0.05:4];
t = cos(k*pi*p) + 3*sin(pi*p);
plot(p, t, '-'), xlabel('时间'); ylabel('输入信号');
% 2.生成BP网络。用newff函数生成前向型BP网络，设定隐层中神经元数目为10
% 分别选择隐层的传递函数为 tansig，输出层的传递函数为 purelin，
% 学习算法为trainlm。
net = newff(minmax(p),[10,10,1],{'tansig','tansig','purelin'},'trainlm');
% 3.对生成的网络进行仿真并做图显示。
y1 = sim(net,p); plot(p, t, '-', p, y1, '--')
% 4.训练。对网络进行训练，设定训练误差目标为 1e-5，最大迭代次数为300，
% 学习速率为0.05。
net.trainParam.lr=0.05;
net.trainParam.epochs=1000;
net.trainParam.goal=1e-5;
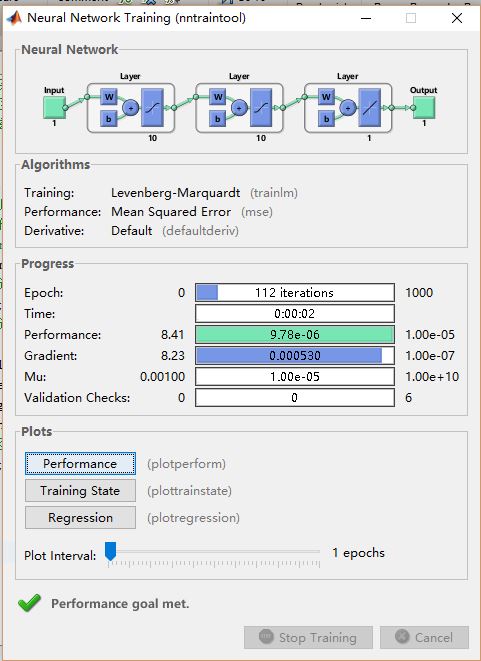
[net,tr]=train(net,p,t);
%5.再次对生成的网络进行仿真并做图显示。
y2 = sim(net,p);
plot(p, t, '-', p, y2, '*')

newff 函数用来生成一个feed-forward backpropagation network

sim 命令运行 simulink 建立的模型，相当于对输入 p 作用模型 net，输出 y2

拟合图像