来自:Eastmount
在我们日常生活中Power Law(幂次分布,Power-law Distributions)是常见的一个数学模型,如二八原则。这个世界上是20%的人掌握80%的人的金钱去经营,20%的人口拥有80%的财富,20%的上市公司创造80%的价值,80%的收入来自20%的商品等。
下图表示人类的财富幂律分布图,极少数人拥有微弱优势的人却拥有天文级别的财富。
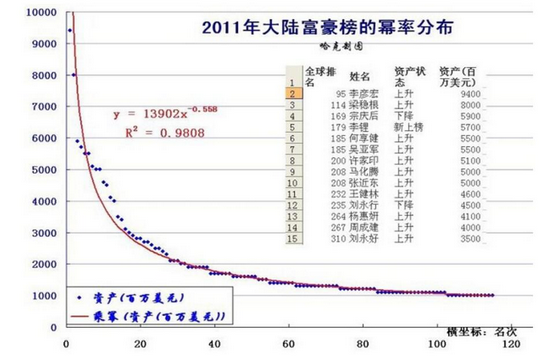
为什么会有这样的差别呢?
这是因为时间的乘积效应,智力上的微弱优势,乘以时间,就会得到价值(财富)几何级的增长。
经济学财富分布满足Pareto Power law tail分布,语言中有词频的幂律分布,城市规模和数量满足幂律分布,音乐中有f分之1噪音(幂律分布)。通常人们理解幂律分布就是所谓的马太效应,二八原则,即少数人聚集了大量的财富,而大多数人的财富数量都很小,因为胜者通吃的原则。
f(x)表示某一数量指标x的发生次数,即幂率分布公式。
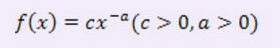

再如钱学森通信反应间隔分布:
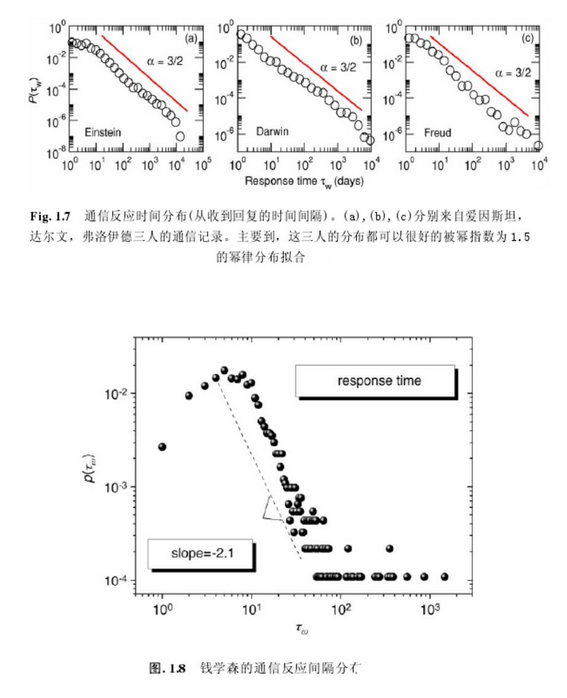







 本文探讨了幂律分布(Power-law Distributions)这一常见数学模型,包括其在经济学、语言学等多个领域的应用,如二八原则及马太效应,并举例说明其在财富分配等方面的具体表现。
本文探讨了幂律分布(Power-law Distributions)这一常见数学模型,包括其在经济学、语言学等多个领域的应用,如二八原则及马太效应,并举例说明其在财富分配等方面的具体表现。
















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








