[LeetCode]Construct Binary Tree from Preorder and Inorder Traversal

最新推荐文章于 2025-08-13 10:25:05 发布

转载最新推荐文章于 2025-08-13 10:25:05 发布 · 75 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/yeqluofwupheng/p/7429781.html

文章标签：

#数据结构与算法

本文介绍了如何利用前序和中序、后序和中序遍历序列来构建二叉树的方法。包括递归和非递归两种实现方式，并提供了详细的代码示例。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

105. Construct Binary Tree from Preorder and Inorder Traversal

Given preorder and inorder traversal of a tree, construct the binary tree.

Note:
You may assume that duplicates do not exist in the tree.

题意;给定前序和中序遍历的序列，构造该二叉树

思路：

前序遍历的序列中每个元素都是一颗子树的根节点，从根节点开始到它的左子树的根节点...

而中序遍历的序列是被根节点分成了前后两部分，前面一半是左子树，后面一半是右子树；

因此，可以以前序序列中的元素为中心来划分中序序列。

例如：

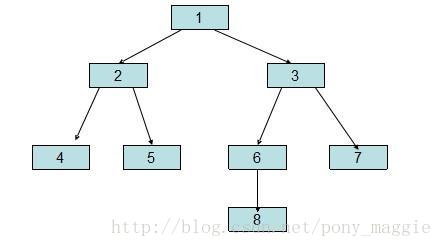
前序遍历：1->2->4->5->3->6->8->7

前序序列中1时整棵树的树根，2是1的左子树的树根，4是2的左子树的树根，5是2的右子树的树根，3是1的右子树的树根......

中序遍历：4->2->5->1->8->6->3->7

中序序列中树根1将其分成{4,2,5}和{8,6,3,7}，{4,2,5}正是1的左子树中的节点，{8,6,3,7}正是1的右子树中的节点；

同样2将{4,2,5}分成两部分，正好对应它的左右子树的节点，因此，可以将两个序列结合起来确定二叉树的结构。

递归的做法

prePos表示当前元素在前序序列中的位置下标；border是中序序列中的一个范围下标，它是当前子树在中序序列中的范围。

prePos = 1，即指向元素2时，border = [0,2]，即包含[4,2,5]三个元素；

prePos = 5，即指向元素6时，border = [4,5]，即包含[8,6]两个元素。

TreeNode* recursiveBuildTree(vector<int>& preorder, vector<int>& inorder, int& prePos, pair<int, int> border){
    //空的情况
    if (!inorder.size())return NULL;
    //避免无左右子树，导致下届比上届还大
    if (border.first > border.second)return NULL;
    if (border.first == border.second){//只剩唯一元素
        TreeNode *root = new TreeNode(inorder.at(border.first));
        return root;
    }
    //生成当前根节点
    TreeNode *root = new TreeNode(preorder.at(prePos));
    int middle = border.first;
    //找到当前根节点在中序遍历中的位置，将它以根节点为界分为左右子树
    while (middle <= border.second && preorder.at(prePos) != inorder.at(middle)){
        middle++;
    }
    pair<int, int>cborder(border.first,middle - 1);//左子树的范围
    root->left = recursiveBuildTree(preorder, inorder, ++prePos, cborder);//寻找左子树
    if (root->left == NULL)prePos--;//若左子树为空，则prePos不应该加一
    cborder.first = middle + 1;
    cborder.second = border.second;
    root->right = recursiveBuildTree(preorder, inorder, ++prePos, cborder);//寻找右子树
    if (root->right == NULL)prePos--;//右子树为空时，prePos不应该加一
    return root;
}

非递归的解法

TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
    //空树的情况
    if (!inorder.size())return NULL;
    TreeNode* root = new TreeNode(preorder.at(0));
    stack<pair<TreeNode*,pair<int,int>>>s;
    int prei = 0;//当前访问的元素在前序序列中的位置
    pair<int, int>border(0,inorder.size() - 1);//当前元素对应在中序序列中的范围
    pair<TreeNode*, pair<int, int>> e0(root,border);
    s.push(e0);
    while (!s.empty()){
        pair<TreeNode*, pair<int, int>> p = s.top();
        int middle = p.second.first;
        //找到当前根节点在中序遍历中的位置，将它以根节点为界分为左右子树
        while (middle <= p.second.second && p.first->val != inorder.at(middle)){
            middle++;
        }
        //没有找到，序列有错，无法得到二叉树
        if (middle > p.second.second)return NULL;
        //左子树为空或为叶节点,或左子树已访问过
        if (middle - 1 <= p.second.first || p.first->left != NULL){
            if (p.first->left == NULL && middle - 1 == p.second.first){//左子树是叶节点
                ++prei;
                TreeNode* left = new TreeNode(inorder.at(middle - 1));
                p.first->left = left;
            }
            s.pop();
            if (middle + 1 == p.second.second){//右子树是叶节点
                ++prei;
                TreeNode* right = new TreeNode(inorder.at(middle + 1));
                p.first->right = right;
            }
            else if (middle + 1 < p.second.second){//进入右子树
                ++prei;
                pair<int, int>rightBorder(middle + 1, p.second.second);
                TreeNode* right = new TreeNode(preorder.at(prei));
                p.first->right = right;
                pair<TreeNode*, pair<int, int>> rightNode(right, rightBorder);
                s.push(rightNode);
            }
        }else{//进入左子树
            ++prei;
            pair<int, int>leftBorder(p.second.first,middle - 1);
            TreeNode* left = new TreeNode(preorder.at(prei));
            p.first->left = left;
            pair<TreeNode*, pair<int, int>> leftNode(left,leftBorder);
            s.push(leftNode);
        }
    }
    return root;
}

106 Construct Binary Tree from Inorder and Postorder Traversal

Given inorder and postorder traversal of a tree, construct the binary tree.

Note:
You may assume that duplicates do not exist in the tree.

题意：给定中序和后序遍历的序列，构造该二叉树

和上面的类似，后序序列是左子树、右子树、树根的顺序遍历，因此，树根必然是最后的一个元素，接着从后往前是右子树、左子树...

因此和前序相反，再结合中序就能确定树的结构。

例如：（还是上面的二叉树）

中序遍历：4->2->5->1->8->6->3->7

后序遍历：4->5->2->8->6->7->3->1

后序序列中最后的一定是树根节点1，然后3是1的右子树的树根，7是3的右子树的树根，6是3的左子树树根，8是6的儿子节点，这个是左孩子还是右孩子要根据中序的序列来确认；

例如如果中序中8在6的前面，则8是6的左孩子；反之则是6的右孩子。

因此，同理能够通过中序和后序序列的到二叉树的结构。

递归的做法

TreeNode* recursiveBuildTree(vector<int>& inorder, vector<int>& postorder, int& postPos, pair<int, int> border){
    //空的情况
    if (!inorder.size())return NULL;
    //避免无左右子树，导致下界比上界还大
    if (border.first > border.second)return NULL;
    if (border.first == border.second){//只剩唯一元素
        TreeNode *root = new TreeNode(inorder.at(border.first));
        return root;
    }
    //生成当前根节点
    TreeNode *root = new TreeNode(postorder.at(postPos));
    int middle = border.first;
    //找到当前根节点在中序遍历中的位置，将它以根节点为界分为左右子树
    while (middle <= border.second && postorder.at(postPos) != inorder.at(middle)){
        middle++;
    }
    pair<int, int>cborder(middle + 1, border.second);//右子树的范围
    root->right = recursiveBuildTree(inorder, postorder, --postPos, cborder);//寻找右子树
    if (root->right == NULL)postPos++;//若右子树为空，则postPos不应该减一
    cborder.first = border.first;
    cborder.second = middle - 1;
    root->left = recursiveBuildTree(inorder, postorder, --postPos, cborder);//寻找左子树
    if (root->left == NULL)postPos++;//左子树为空时，postPos不应该减一
    return root;
}

非递归的做法

TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder){
    //空树的情况
    if (!inorder.size())return NULL;
    int prei = postorder.size() - 1;//当前访问的元素在后序序列中的位置
    TreeNode* root = new TreeNode(postorder.at(prei));
    stack<pair<TreeNode*, pair<int, int>>>s;
    pair<int, int>border(0, inorder.size() - 1);//当前元素对应在中序序列中的范围
    pair<TreeNode*, pair<int, int>> e0(root, border);
    s.push(e0);
    while (!s.empty()){
        pair<TreeNode*, pair<int, int>> p = s.top();
        int middle = p.second.first;
        //找到当前根节点在中序遍历中的位置，将它以根节点为界分为左右子树
        while (middle <= p.second.second && p.first->val != inorder.at(middle)){
            middle++;
        }
        //没有找到，序列有错，无法得到二叉树
        if (middle > p.second.second)return NULL;
        //右子树为空或为叶节点,或右子树已访问过
        if (middle + 1 >= p.second.second || p.first->right != NULL){
            if (p.first->right == NULL && middle + 1 == p.second.second){//右子树是叶节点
                --prei;
                TreeNode* right = new TreeNode(inorder.at(middle + 1));
                p.first->right = right;
            }
            s.pop();
            if (middle - 1 == p.second.first){//左子树是叶节点
                --prei;
                TreeNode* left = new TreeNode(inorder.at(middle - 1));
                p.first->left = left;
            }
            else if (middle - 1 > p.second.first){//进入左子树
                --prei;
                pair<int, int>leftBorder(p.second.first, middle - 1);
                TreeNode* left = new TreeNode(postorder.at(prei));
                p.first->left = left;
                pair<TreeNode*, pair<int, int>> leftNode(left, leftBorder);
                s.push(leftNode);
            }
        }
        else{//进入右子树
            --prei;
            pair<int, int>rightBorder(middle + 1, p.second.second);
            TreeNode* right = new TreeNode(postorder.at(prei));
            p.first->right = right;
            pair<TreeNode*, pair<int, int>> rightNode(right, rightBorder);
            s.push(rightNode);
        }
    }
    return root;
}