csa Round #73 (Div. 2 only)

最新推荐文章于 2025-09-12 17:31:31 发布

转载最新推荐文章于 2025-09-12 17:31:31 发布 · 88 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/BobHuang/p/8571324.html

文章标签：

#数据结构与算法

本文精选了几道算法竞赛题目并提供了详细的解决方案，包括最小化成本使数组元素相等、求小球高度和最小值、判断二叉树同构性、俄罗斯套娃组合数量以及寻找特定子字符串等问题。

Three Equal

Time limit: 1000 ms
Memory limit: 256 MB

You are given an array $A_i = ((A_i + 1)\ \% \ 3)Ai=((Ai+1) % 3).$

Find the minimum cost to make all elements equal.

Standard input

The first line contains one integer

The second line contains

Standard output

Output a single number representing the minimum cost to make all elements of

Constraints and notes

$\leq N \leq 10^31≤N≤103$
The elements of the array

Input	Output
4 1 0 0 2	3
3 1 2 2	1
3 1 1 1	0

问你n个数到一个相同模数的最小值，那就直接枚举这三个模数好了，当时手残还打错一个字母

#include <bits/stdc++.h>
using namespace std;
int b[4];
int main()
{
    int n;
    cin>>n;
    for(int i=0,x;i<n;i++)
    {
        if(x%3==0)b[1]+=2,b[2]+=2;
        else if(x%3==1)b[0]+=2,b[3]+=1;
        else b[1]+=1,b[2]+=2;
    }
    cout<<min(min(b[0],b[1]),b[2]);
    return 0;
}

Ricocheting Balls

Time limit: 1000 ms
Memory limit: 256 MB

There are $i^{\text{th}}ith ball is H_iHi meters above the ground. The balls are supposed to be falling at 11 meter per second, but they're not; they're stuck in time, hovering.$

You can repeat the following process as many times as you want (possibly

If a ball hits the ground, which is situated at the height level

You want to find the moment of time that minimizes the sum of heights of all the balls. Print the value of the sum obtained at this moment of time.

Standard input

The first line contains an integer

The next line contains

Standard output

Print an integer, the minimum sum of heights of all balls that can be obtained by the above-described process.

Constraints and notes

$\leq N \leq 10^51≤N≤105$
$\leq H_i \leq 10^91≤Hi≤109$

Input	Output	Explanation
4 1 4 5 2	6	Moment of time Moment of time Moment of time Moment of time
9 1 7 1 1 1 5 3 6 3	17

小球每1s落下1m，问你这个距离地面距离的最小和，当然是选择中位数了

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int h[N];
int main()
{
    int n;
    cin>>n;
    long long ans=0;
    for(int i=0; i<n; i++)cin>>h[i];
    sort(h,h+n);
    for(int i=0; i<n; i++)
        ans+=abs(h[i]-h[(n-1)/2]);
    cout<<ans<<endl;
    return 0;
}

Binary Isomorphism

Time limit: 1000 ms
Memory limit: 256 MB

You are given two binary trees. These two trees are called isomorphic if one of them can be obtained from other by a series of flips, i.e. by swapping the children of some nodes. Two leaves are isomorphic.

Both these trees will be given through their parents array. In a parents array,

nodes are
there is only one position $P_r = 0Pr=0. This means that rr is the root of the tree.$
for every node $\neq ri≠r, its direct parent is P_iPi.$

Standard input

The first line contains

For every test:

the first line contains
the second line contains
the third line contains

Standard output

For every test case, print a line containing 1 if the two trees are isomorphic, or 0 otherwise.

Constraints and notes

$\leq T \leq 201≤T≤20$
$\leq N \leq 10^51≤N≤105. The sum of all values of NN in a test is \leq 10^5≤105$

Input	Output	Explanation
3 4 3 0 2 3 3 4 0 3 5 5 1 0 3 4 5 1 4 2 0 5 0 1 2 1 4 0 1 4 1 2	0 1 1	13243142 1523442351 1234512543

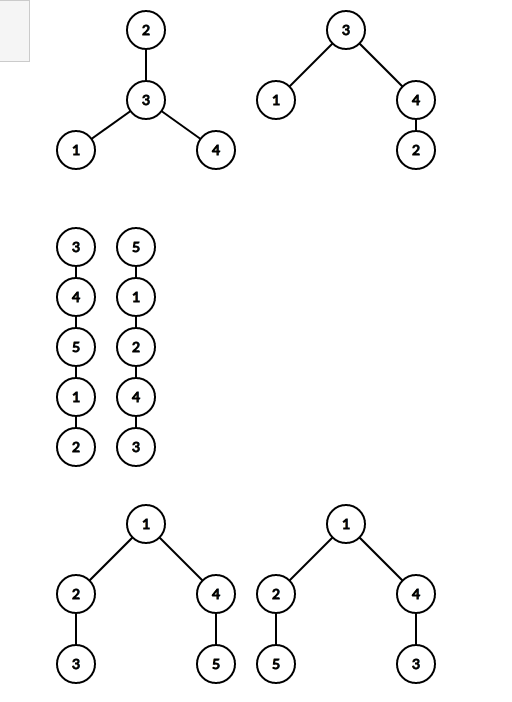
给你两个二叉树，看其是否同构

需要dfs看其每个节点孩子数是否相同

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+5;
vector<int>v[N];
vector<int>v2[N];
int dfs(int x,int y)
{
    if(v[x].size()!=v2[y].size())return 0;
    if(v[x].size()==0)return 1;
    if(v[x].size()==1)return dfs(v[x][0],v2[y][0]);
    else
    {
        if(dfs(v[x][0],v2[y][0])&&dfs(v[x][1],v2[y][1])||dfs(v[x][0],v2[y][1])&&dfs(v[x][1],v2[y][0]))
            return 1;
        return 0;
    }
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        int n,rt1,rt2;
        scanf("%d",&n);
        for(int i=1; i<=n; i++)
            v[i].clear(),v2[i].clear();
        for(int i=1; i<=n; i++)
        {
            int x;
            scanf("%d",&x);
            if(x==0)
                rt1=i;
            else v[x].push_back(i);
        }
        for(int i=1; i<=n; i++)
        {
            int x;
            scanf("%d",&x);
            if(x==0)
                rt2=i;
            else v2[x].push_back(i);
        }
        printf("%d\n",dfs(rt1,rt2));
    }
    return 0;
}

还可以去括号匹配的思想

#include <bits/stdc++.h>
#define mod 1000000007
#define p 666013
using namespace std;

int put[300010];
vector <int> adia[200010];

pair <int, int> dfs(int nod) {
    vector <pair <int, int>> fii;
    for (auto i : adia[nod]) {
        fii.push_back(dfs(i));
    }

    sort(fii.begin(), fii.end());
    int lact(1);
    int ans = '(';
    for (auto i : fii) {
        ans += 1ll * i.first * put[lact] % mod;
        lact += i.second;
    }
    ans += 1ll * ')' * lact;
    lact++;
    return { ans, lact };
}

void solve()
{
    int n;
    cin >> n;
    vector <pair <int, int>> v;

    for (int q(0); q < 2; q++) {
        for (int i(1); i <= n; i++)
            adia[i] = vector <int> ();

        int root;
        for (int i(1); i <= n; i++) {
            int tata;
            cin >> tata;
            if (tata == 0)
                root = i;
            else
                adia[tata].push_back(i);
        }
        auto x = dfs(root);
        v.push_back(x);
    }

    cout << (v[0] == v[1]) << '\n';
}


int main() {
    put[0] = 1;

    for (int i(1); i < 300010; i++)
        put[i] = 1ll * 666013 * put[i - 1] % mod;
    int t;
    cin >> t;

    while (t--)
        solve();
    return 0;
}

Russian Dolls Ways

Time limit: 1000 ms
Memory limit: 256 MB

You have $i^{th}ith doll you know its size A_iAi.$

A doll of size

For example, if you have three dolls of sizes

Your goal is to count the number of nestings that minimizes the number of dolls at the end.

Consider the array $P_iPi is index of the doll in which the doll ii is nested into. If doll iiis not nested into any other doll, P_i = 0Pi=0. Two ways are considered distinct if there is a 1 \leq i \leq N1≤i≤Nsuch that P1_i \neq P2_iP1i≠P2i.$

Standard input

The first line contains a single integer

The second line contains

Standard output

Output a single number representing the number of ways to nest the dolls in order to achieve the minimum number of dolls at the end, modulo $10^9+7109+7.$

Constraints and notes

$\leq N \leq 10^51≤N≤105$
$\leq A_i \leq 10^91≤Ai≤109$

Input	Output	Explanation
3 1 2 3	1	The minimum number of dolls at the end is
4 1 2 2 3	4	The minimum number of dolls at the end is The
6 1 1 2 2 3 3	4	The minimum number of dolls at the end is The

俄罗斯套娃，就是让你求一下这个长度为n的序列最多能分成几个序列，其实就是重复个数最多的那个个数k

然后就是每个值都要选一个大小为k的盒子

#include<bits/stdc++.h>
using namespace std;
const int MD=1e9+7;
long long ans=1;
unordered_map<int,int> M;
vector<int>V;
int main() {
    ios_base::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    int n;
    cin>>n;
    for(int i=0,x;i<n;i++)cin>>x,M[x]++;
    for(auto X:M)V.push_back(X.second);
    sort(V.begin(),V.end());
    int k=*V.rbegin();
    V.pop_back();
    for(auto X:V)
        for(int i=0;i<X;i++)ans=ans*(k-i)%MD;
    cout<<ans;
}

Strange Substring

Time limit: 2000 ms
Memory limit: 256 MB

You are given two strings

Standard input

The first line contains

The second line contains

Standard output

Print the answer on the first line.

Constraints and notes

$\leq |A|, |B| \leq 10^51≤∣A∣,∣B∣≤105$

Input	Output
abcab bcab	3
aaa aa	1
acabad abcacd	12

题意很好理解，就是让你找是A的子串，但是不是B的子串的个数

benq的SA+LCP

#include <iostream>
#include <cstring>
#include <vector>
#include <algorithm>
 
using namespace std;
 
struct suffix_array {
suffix_array(const char* S) : N(strlen(S)) {
  vector<int> V;
  for(int i = 0; i < N; i++) V.push_back(S[i]);
  init(V);
}
 
suffix_array(const vector<int>& VV) : N(VV.size()) {
  vector<int> V(VV);
  init(V);
}
 
int N;
vector<int> SA;
vector<int> RA;
 
void compress(vector<int>& V, vector<int>& C) {
  copy(V.begin(), V.end(), C.begin());
  sort(C.begin(), C.end());
  auto cend = unique(C.begin(), C.end());
  for(int i = 0; i < N; i++) {
    V[i] = lower_bound(C.begin(), cend, V[i]) - C.begin() + 1;
  }
  V.push_back(0); C.push_back(0);
}
 
void compute_sa(vector<int>& V, vector<int>& C) {
  vector<int> T(N + 1);
  for(int i = 0; i <= N; i++) SA.push_back(i);
  for(int ski = 0; V[SA[N]] < N; ski = ski ? ski << 1 : 1) {
    fill(C.begin(), C.end(), 0);
    for(int i = 0; i < ski; i++) T[i] = N - i;
    for(int i = 0, p = ski; i <= N; i++) if(SA[i] >= ski) T[p++] = SA[i] - ski;
    for(int i = 0; i <= N; i++) C[V[i]]++;
    for(int i = 1; i <= N; i++) C[i] += C[i - 1];
    for(int i = N; i >= 0; i--) SA[--C[V[T[i]]]] = T[i];
    
    T[SA[0]] = 0;
    for(int j = 1; j <= N; j++) {
      int a = SA[j];
      int b = SA[j - 1];
      T[a] = T[b] + (a + ski >= N || b + ski >= N ||
                     V[a] != V[b] || V[a + ski] != V[b + ski]);
    }
    V.swap(T);
  }
}
 
void compute_lcp(const vector<int>& OV) {
  LCP = vector<int>(N);
  int len = 0;
  for(int i = 0; i < N; i++, len = max(0, len - 1)) {
    int si = RA[i];
    int j = SA[si - 1];
    for(; i + len < N && j + len < N && OV[i + len] == OV[j + len]; len++);
    LCP[si - 1] = len;
  }
}
 
void init(vector<int>& V) {
  vector<int> OV(V);
  vector<int> C(N);
  compress(V, C);
  compute_sa(V, C);
  RA.resize(N + 1);
  for(int i = 0; i <= N; i++) RA[SA[i]] = i;
  compute_lcp(OV);
}
  
vector<int> LCP;
};
 
int main() {
  ios_base::sync_with_stdio(false);
 
  string S;
  vector<pair<int, int> > A;
 
  int N = 2;
  for (int i = 0; i < N; i++) {
    string T; cin >> T;
 
    S += T;
    S += "?";
    for (int j = 0; j < T.size(); j++) {
      A.push_back(make_pair(i, T.size() - j));
    }
    A.push_back(make_pair(-1, -1));
  }
  A.push_back(make_pair(-1, -1));
 
  vector<long long> result(N);
  suffix_array sa(S.c_str());
  sa.LCP.push_back(0);
  for (int i = 1; i <= sa.N; ) {
    int j = sa.SA[i];
    int ind = A[j].first;
    if (ind == -1) {
      ++i;
      continue;
    }
    int sz = 1;
    while (i + sz <= sa.N && A[sa.SA[i + sz]].first == ind) {
      ++sz;
    }
 
    int ln = sa.LCP[i - 1];
    for (int j = i; j < i + sz; j++) {
      result[ind] += max(A[sa.SA[j]].second - max(ln, sa.LCP[j]), 0);
      ln = min(ln, sa.LCP[j]);
    }
    i += sz;
  }
  cout << result[0];
 
  return 0;
}

一种我倾向于的写法

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#define N 2000000
using namespace std;
struct node{
    int son[27];
    int len,fail;
    bool sig;
}tri[N];
char S[N];
int len,L,lst;
int in[N],d[N];
void add(int last,int c,bool sig){
    static int v,u,up,up1;
    v=++L;
    u=last;
    tri[v].len=tri[u].len+1;
    for (;u&&!tri[u].son[c];u=tri[u].fail)tri[u].son[c]=v;
    if (!u)tri[v].fail=1;
    else{
        up=tri[u].son[c];
        if (tri[up].len==tri[u].len+1)tri[v].fail=up;
        else{
            up1=++L;
            tri[up1]=tri[up];
            tri[up1].len=tri[u].len+1;
            tri[up].fail=tri[v].fail=up1;
            for (;u&&tri[u].son[c]==up;u=tri[u].fail)tri[u].son[c]=up1;
        }
    }
    tri[v].sig=sig;
    lst=v;
}
int main(){
    scanf(" %s",S+1);
    len=strlen(S+1);
    lst=1,L=1;
    for (int i=1;i<=len;i++)add(lst,S[i]-'a',0);
    scanf(" %s",S+1);
    len=strlen(S+1);
    add(lst,26,1);
    for (int i=1;i<=len;i++)add(lst,S[i]-'a',1);
    for (int i=1;i<=L;i++)in[tri[i].fail]++;
    int l=0,r=0;
    for (int i=1;i<=L;i++)
        if (!in[i])d[++r]=i;
    while (l!=r){
        ++l;
        tri[tri[d[l]].fail].sig|=tri[d[l]].sig;
        if (!(--in[tri[d[l]].fail]))
            d[++r]=tri[d[l]].fail;
    }
    long long ans=0;
    for (int i=1;i<=L;i++)
        if (!tri[i].sig)
            ans+=tri[i].len-tri[tri[i].fail].len;
    printf("%lld\n",ans);
    return 0;
}