分类算法

一，分类问题（又叫做预测问题，预测的对象是数值类型）

　　训练集（用来构建模型，拟合模型，可以训练出很多个模型）——>使用模型：测试集（仅仅一次使用，评估模型泛化的性能），验证集（进行模型的选择选择特征，调参，防止过拟合，多次使用，以不断调参），这些都是已知table的

　　分类问题的本质是，根据一些属性去分标签属性

　　

 

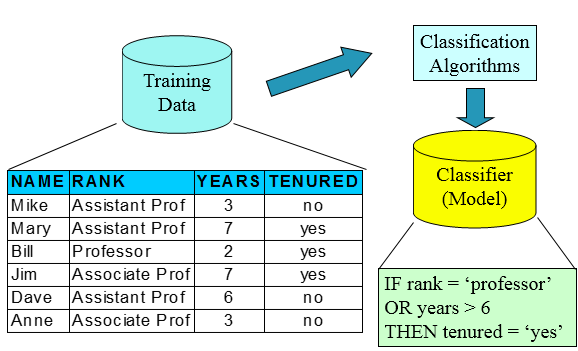
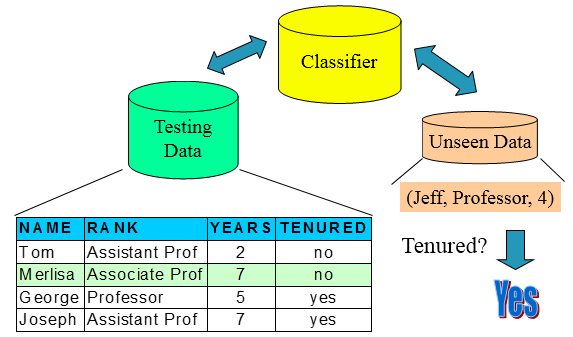
 二，决策树

　　根据输入，从树的根最后在树里面走一遍到输出的叶子节点，得到分类结果。分类的目的是让不确定性消失，使熵下降最快，使子节点的纯度最高。

• 　　步鄹：（1）将所有数据都放在根节点，

　　　　　（2）选择一个特征进行分解出子节点

　　　　　（3）在子节点上判断是否不再分裂，如果不再分裂则直接给出这个子节点的分类结果（这个子节点的多数table为这个节点的输出table），否则继续选择一个特征进行分解（即到第二步）

• 　　算法的核心：最优分裂特征（节点）的选取；分裂成几类；什么时候停止分裂。
• 　　分裂特征的选取：ID3算法，C4.5算法（可以用来决定分裂成几类，即最优分裂值的选取），CART树

　　（1）ID3：使信息增益最大。（熵下降最快）

　　父节点的熵-子节点的熵

　　

    InfoA是分类之后的，分别求各子节点的熵，再乘上各子节点概率。

　　注意：根节点计算的时候，Info(D)是算没有任何条件的分类结果的概率

 （2）C4.5：使信息增益率最大（减弱ID3的缺点，ID3偏向于选择多分支，因为多分支意味着纯度高）

 

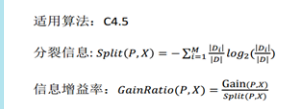
分母 是把子节点看成整体，算出分裂成子节点之后的整体的熵。

 例题：

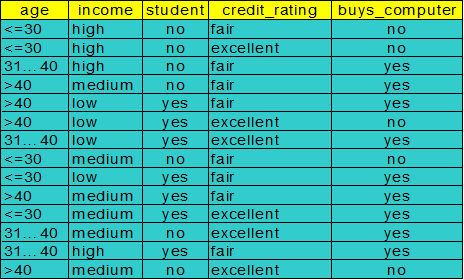
要分类的标签table：buys_computer：no or yes

选取第一个节点：

Info income(D)=4/14*I(2,2)+6/14*I(3,1)+4/14*i(3,1)

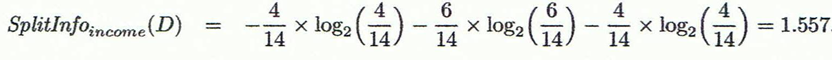
(3)CARt树

　　基尼系数：衡量子节点的纯度，基尼系数越小，纯度越高（其实和熵的意思差不多）

　　分成子节点的GINI系数，是要分别求GINI再对概率的加权求和。

 

回归树（输入是连续值）：

　　先划分节点，将数据集分裂：在整个区间内取一个点，将区间分为两部分，使损失函数最小。

https://blog.youkuaiyun.com/weixin_40604987/article/details/79296427

　　

参考：https://www.cnblogs.com/fionacai/p/5894142.html

https://www.cnblogs.com/wenyi1992/p/7685131.html

 

转载于:https://www.cnblogs.com/yttas/p/10023229.html