1模型表达(MODEL REPRESENTATION)
以之前的房屋交易问题为例,假使我们回归问题的训练集(Training Set)如下表所示:
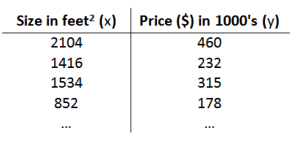
我们将要用来描述这个回归问题的标记如下:
m 代表训练集中实例的数量
x 代表特征/输入变量
y 代表目标变量/输出变量
(x,y) 代表训练集中的实例
(x (i) ,y (i) ) 代表第 i 个观察实例
h 代表学习算法的解决方案或函数也称为假设(hypothesis)
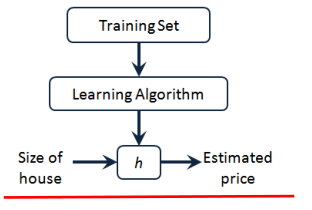
因而,要解决房价预测问题,我们实际上是要将训练集“喂”给我们的学习算法,进而学习得
一个假设 h,然后将我们要预测的房屋的尺寸作为输入变量输入给 h,预测出该房屋的交易价
格作为输出变量输出为结果。
12
那么,对于我们的房价预测问题,我们该如何表达 h?
一种可能的表达方式为:![]()
因为只含有一个特征/输入变量,因此这样的问题叫作单变量线性回归问题。
2 代价函数(COST FUNCTION)
我们现在要做的便是为我们的模型选择合适的参数(parameters)θ 0 和θ 1, 在房价问题这个
例子中便是直线的斜率和在 y 轴上的截距。
我们选择的参数决定了我们得到的直线相对于我们的训练集的准确程度,模型所预测的值与训
练集中实际值之间的差距(下图中蓝线所指)就是建模误差(modeling error)。
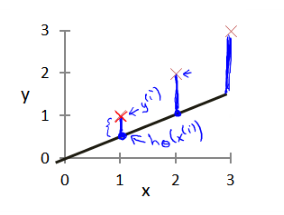
我们的目标便是选择出可以使得建模误差的平方和能够最小的模型参数。
即使得代价函数 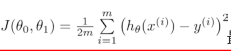 最小。
最小。
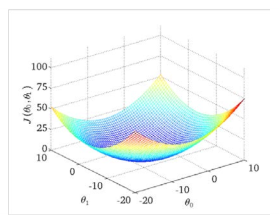
我们绘制一个等高线图,三个坐标分别为θ 0 和θ 1 和 J(θ 0, θ 1 ):
则可以看出在三维空间中存在一个使得 J(θ 0, θ 1 )最小的点。
梯度下降是一个用来求函数最小值的算法,我们将使用梯度下降算法来求出代价函数 J(θ 0, θ 1 )
的最小值。
梯度下降背后的思想是:开始时我们随机选择一个参数的组合(θ 0, θ 1,..., θn),计算代价函数,
然后我们寻找下一个能让代价函数值下降最多的参数组合。可以想象成从山上某点往山下走的过程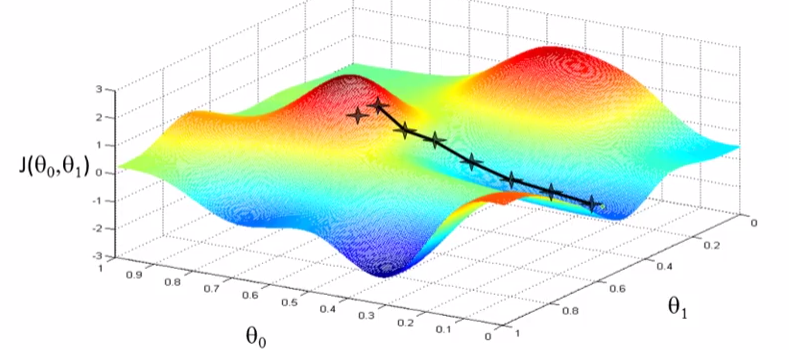 在起点相处环顾四周选择认为能最快下山的路(最陡),到达一个新的起点,如此重复直到最低点。
在起点相处环顾四周选择认为能最快下山的路(最陡),到达一个新的起点,如此重复直到最低点。
我们持续这么做直到到到一个局部最小值(local minimum),因为我们并没有尝试完所有的参数组合,所以不能确定我们得到的局部最小值是否便是全局最小值(global minimum),选择不同的初始参数组合,可能会
找到不同的局部最小值。
梯度下降算法的定义:
其中 :=为赋值号,![]() 是一个数字称为学习速率,表示下山例子中的一步下山走的路长短
是一个数字称为学习速率,表示下山例子中的一步下山走的路长短
在此基础上不断更新![]() 直到收敛。
直到收敛。
 此为一次更新θ 0和θ 1。需要同步更新,不能先
此为一次更新θ 0和θ 1。需要同步更新,不能先![]() 再
再![]() 。
。
例题:



通常的代价函数的图形都是形如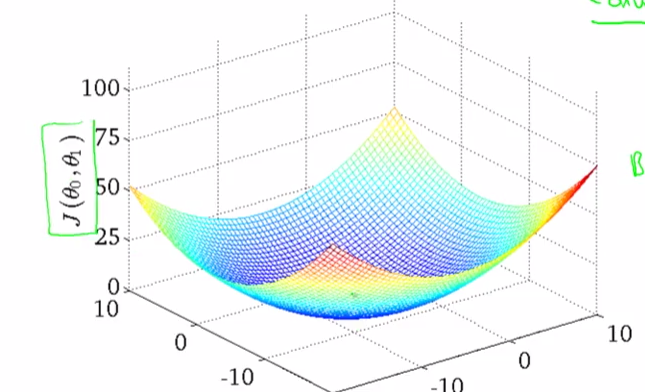 的碗型,只有一个极小值,因此对代价函数使用梯度下降通常都能得到这个最小值点。
的碗型,只有一个极小值,因此对代价函数使用梯度下降通常都能得到这个最小值点。
以上的梯度下降有时候也称为批量梯度下降,指的是在每一步梯度下降中我们都用到了所有的训练样本。
当然有时候的梯度下降并不是考虑所有的训练样本,而是只选取其中的一个子集




 本文通过房价预测问题引入单变量线性回归概念,并详细解释了如何利用梯度下降法来选择合适的模型参数,以实现对数据的最佳拟合。
本文通过房价预测问题引入单变量线性回归概念,并详细解释了如何利用梯度下降法来选择合适的模型参数,以实现对数据的最佳拟合。

















 672
672

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








