LeetCode 51 N-Queens

题目

The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other.

image

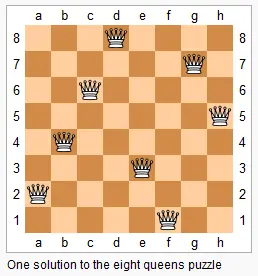
Given an integer n, return all distinct solutions to the n-queens puzzle.

Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space respectively.

Example:

Input: 4
Output: [
[".Q..", // Solution 1
"...Q",
"Q...",
"..Q."],
["..Q.", // Solution 2
"Q...",
"...Q",
".Q.."]
]
Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above.

---

解法思路（一）

皇后之间不能相互攻击什么意思？

• 皇后之间不能在同一行，同一列，同一对角线；

最后的解有什么样的特征？

• 每一行只有一个皇后；
• 每一列只有一个皇后；
• 每一对角线只有一个皇后；

二维数组的对角线有什么特征？

• 每一条从右上到左下的对角线，横纵坐标相加之和是一个常数；
• 每一条从左上到右下的对角线，横纵坐标相减之差是一个常数；

如何回溯的找所有解？

• 一行一行的放皇后；
• 第一行放过皇后的列，第二行的皇后就不能放在这一列，故用一个数组 col 记录哪些行上放过皇后；
• 同时，当一个皇后被放置后，有两条对角线上也不能再放皇后了；
• 两个方向的所有对角线是否有皇后，用两个布尔数组 dia1 和 dia2 表示；
• dia1 表示从右上到左下的所有对角线，坐标 (row, col) 处于哪个对角线上，dia1[row + col] 就是的；
• dia2 表示从左上到右下的所有对角线，坐标 (row, col) 处于哪个对角线上，dia2[row - col + n - 1] 就是的；
• 每一行可以在哪落皇后，都是根据 col dia1 dia2 的限制决定的，每一行可以落皇后的位置可以有多个，先在第一个位置落，如果进行到下一行发现落哪都不成了，那么回退到上一行，在下一个可以落皇后的位置落皇后，再去下一行落皇后，直到在最后一行成功落下皇后，一个解就找到了；
• 然后再一行行的向上回溯，回溯到每一个位置，都将该位置所处的 col dia1 dia2 置为未占用的状态，然后在该行能放皇后的下一个位置放置皇后，直到该行所有能放置皇后的位置都放过了，然后回溯到上一行，将上一行能放置皇后的位置都试一遍，直到回溯到第一行的最后一个能放皇后的位置也试过了，那么所有的解就都找到了；

解法实现（一）

时间复杂度

• O(n^n)；

空间复杂度

• O(n)；

关键字

N Queens 回溯 递归 二维数组 对角线

实现细节

• Arrays.fill(row, '.'); 给一个 char 数组填充值的 API，比较少用，标出以注意；
• LinkedList 才有 addLast(E e) 和 removeLast() 这样的 API，加以注意；
• dia2[rowIndex - i + n - 1] 用以表示从左上到右下的所有对角线的数组，横纵坐标相减再加上个 n - 1 的偏移量就对应到 dia2 上了；
• res 作为收集解的仓库，存在于递归方法之外；

package leetcode._51;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.List;

public class Solution51_1 {

    private boolean[] cols;
    private boolean[] dia1;
    private boolean[] dia2;
    private ArrayList<List<String>> res;

    public List<List<String>> solveNQueens(int n) {

        cols = new boolean[n];
        // 表示从右上到左下的所有对角线上是否有皇后
        dia1 = new boolean[2 * n - 1];
        // 表示从左上到右下的所有对角线上是否有皇后
        dia2 = new boolean[2 * n - 1];
        res = new ArrayList<>();

        LinkedList<Integer> chessboard = new LinkedList<>();
        putQueen(n, 0, chessboard);

        return res;
    }

    private void putQueen(int n, int rowIndex, LinkedList<Integer> chessboard) {

        if (n == rowIndex) {
            res.add(generateOneSolution(n, chessboard));
            return;
        }

        for (int i = 0; i < n; i++) {
            if (!cols[i] && !dia1[rowIndex + i] && !dia2[rowIndex - i + n - 1]) {
                chessboard.addLast(i);
                cols[i] = true;
                dia1[rowIndex + i] = true;
                dia2[rowIndex - i + n - 1] = true;
                putQueen(n, rowIndex + 1, chessboard);
                dia2[rowIndex - i + n - 1] = false;
                dia1[rowIndex + i] = false;
                cols[i] = false;
                chessboard.removeLast();
            }
        }

        return;
    }

    private List<String> generateOneSolution(int n, List<Integer> chessboard) {

        assert n == chessboard.size();

        ArrayList<String> oneSolution = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            char[] row = new char[n];
            Arrays.fill(row, '.');
            row[chessboard.get(i)] = 'Q';
            oneSolution.add(new String(row));
        }

        return oneSolution;
    }

}

返回 LeetCode [Java] 目录