LeetCode 77 Combinations

题目

Given two integers n and k, return all possible combinations of k numbers out of 1 ... n.

Example:

Input: n = 4, k = 2
Output:

[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

---

解法思路（一）

• 组合；
• 回溯；
• 相当于求 C ²₄；
• 注意组合和排列的区别，对排列来说，[1, 2] 和 [2, 1] 是不同的排列，对组合来说是同一个组合；
• 当输入给出时，一棵树就形成了，比如输入：4, 2，形成的树如下：

    

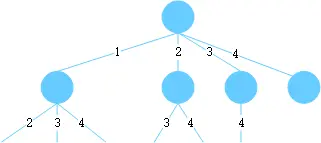
算法过程.png

• 问题转化为求这棵树长度为 2 的路径；

解法实现（一）

时间复杂度

• O(n^k)；

空间复杂度

• O(k)；

关键字

递归 回溯 树 长度为 k 的路径数 深复制

实现细节

• start 控制当前层可以纳入组合的边从第几位开始；
• 下一层可用来纳入组合的边，只能从当前边的右边剩余的边中找，i 是当前边，i + 1 是当前边的右边；

package leetcode._77;

import java.util.LinkedList;
import java.util.List;

public class Solution77_1 {

    private LinkedList<List<Integer>> res;

    public List<List<Integer>> combine(int n, int k) {

        res = new LinkedList<>();
        if (n <= 0 || k <= 0 || k > n) {
            return res;
        }

        LinkedList<Integer> c = new LinkedList<>();
        findCombination(n, k, 1, c);

        return res;
    }

    private void findCombination(int n, int k, int start, LinkedList<Integer> c) {

        if (c.size() == k) {
            res.addLast((List<Integer>)c.clone());
            return;
        }

        for (int i = start; i <= n; i++) {
            c.addLast(i);
            findCombination(n, k, i + 1, c);
            c.removeLast();
        }

        return;
    }

}

---

解法思路（二）

剪枝

• 不可能得到解的路径就不去遍历了，相当于把这样的路径从树中剪掉，所谓剪枝；

结论

• 循环中，i 不一定非要走到最右端 n，走到 n - (k - c.size) + 1 就可以了；

推导过程

• k 是递归的深度，也是组合要求的长度；
• c.size() 是在找长度为 k 的组合的过程中，已经找到了多少个元素；
• k - c.size 是还要找到几个元素才能找出一个有 k 个元素的组合；
• 拿 C²₄ 来说，看第一层，要找到一个 2 个元素的组合，就是在第一层找一个元素，然后在第二层，从剩余的元素中找再找一个元素，相当于在第一层中找俩元素；
• 而且找的规则是这样的：如果第一个元素找的是第 i 个元素，那么第二个元素最左得从 i + 1 找；
• 那么保证能取出两个元素的 i 的最右端在哪呢？
• 4 - (2 - 0) 距最右边界隔着俩元素，再右移一位 4 - (2 - 0) + 1，距最右隔一个位置，加上这个位置本身一共可以填 2 个元素，这个位置就是保证能取出两个元素的 i 的最右的位置；
• (2 - 0) 是 (k - c.size)；
• 4 是 n；
• 这个位置一般化就是：n - (k - c.size) + 1；
• n - (k - c.size) + 1 是小于等于 n 的，进而达到剪枝的目的，进而达到了优化性能的目的；

解法实现（二）

时间复杂度

• O(n^k)；

空间复杂度

• O(k)；

关键字

树 剪枝 递归 回溯

实现细节

• 只把 n 变成了 n - (k - c.size) + 1；

package leetcode._77;

import java.util.LinkedList;
import java.util.List;

public class Solution77_2 {

    private LinkedList<List<Integer>> res;

    public List<List<Integer>> combine(int n, int k) {

        res = new LinkedList<>();
        if (n <= 0 || k <= 0 || k > n) {
            return res;
        }

        LinkedList<Integer> c = new LinkedList<>();
        findCombination(n, k, 1, c);

        return res;
    }

    private void findCombination(int n, int k, int start, LinkedList<Integer> c) {

        if (c.size() == k) {
            res.addLast((List<Integer>)c.clone());
            return;
        }

        for (int i = start; i <= n - (k - c.size()) + 1; i++) {
            c.addLast(i);
            findCombination(n, k, i + 1, c);
            c.removeLast();
        }

        return;
    }

}

返回 LeetCode [Java] 目录