简述相关与回归分析的关系_相关与回归分析入门

变量之间，数量上存在两种关系，一种是确定性的函数关系，一种是不确定性的相关关系。相关分析与回归分析是研究变量之间相关关系的两种基本方法。所谓相关分析，就是用一个指标来表明变量间相互关系的密切程度。所谓回归分析，是根据相关关系的具体形态，选择一个合适的数学模型，来近似表达变量间的数量影响关系。本文以两变量为例加以阐述。

一、基本概念

(一)自变量与因变量

在确定性函数关系中，当某一变量取一定的值时，另一变量有确定值与之相对应，一般把作为影响因素的变量称为自变量，把发生对应变化的变量称为因变量。

(二)相关图

又称散点图，是用来反映两变量之间相关关系的图形。它以直角坐标系的横轴和纵轴分别代表两个变量，将变量值用坐标点的形式描绘出来。相关图是研究相关关系的直观工具，在进行详细的定量分析之前，一般可借助相关图大致判断变量之间是否存在相关关系，以及相关关系的方向、形式和密切程度。

(三)相关系数

是研究两变量之间线性相关程度所采用的尺度，表现为一个常数，记作r。

需要特别说明的是：①r的取值介于-1到1之间；②r是对变量之间线性关系的度量。r=0只表明两变量间不存在线性关系，对非线性关系是否存在无法判断；③r>0，变量间存在正相关，r<0，变量间存在负相关。

二、联系与区别

表1 相关分析与回归分析的联系与区别

三、案例分析

本文利用1996-2009年和2013-2019年我国城镇居民人均年消费性支出和人均年可支配收入的有关年度数据(单位：千元)，以人均消费支出作为因变量Y，人均可支配收入作为自变量X，对两变量进行相关分析和回归分析。(数据后附)

(一)相关图分析

图1 1996-2009年和2013-2019年我国城镇居民人均消费支出Y和人均可支配收入X的相关图

从图1可以看出，当自变量X有着增加的趋势，Y会随着X的增加而增加，说明变量Y和X具有向相同方向变动的趋势，大致判断二者之间存在正相关关系。但是单独根据散点图做出的判断不足以让人信服，需要进一步计算二者的相关系数来判断二者的相关程度。

(二)相关分析

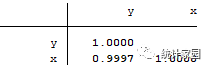
图2 我国城镇居民人均消费支出Y和人均可支配收入X的相关系数r

图2显示，X和Y的相关系数为0.9997，这表明二者之间存在着高度的线性相关关系，这和我们根据散点图做出的大致判断一致。由于二者间存在着高度的相关关系，因此进一步研究二者间相关关系的具体形式即进行回归分析，很有意义。

(三)回归分析(一元线性回归分析)

图3 我国城镇居民人均消费支出Y关于人均可支配收入X的回归结果

图3是令Y关于X作线性回归的结果，得到的Y关于X的回归模型为：

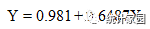
回归结果显示：样本回归系数0.6487通过了显著性检验，说明城镇居民人均可支配收入X对城镇人均消费性支出Y 的影响是非常显著的。同时模型的R2=0.9994，说明模型的拟合程度较高。从实践经验判断，收入越高，消费越大，模型也能很好地解释现实现象。

建立的回归模型具有经济意义，同时有较高的拟合程度，因此可以对未来时期进行简单回归预测，回归预测的基本公式为：

假设2020年城镇居民人均可支配收入为45000元，根据回归预测公式，可以知道：2020年城镇人均消费性支出的预测值为：

四、特别说明

尽管回归分析的结果，是得到了一个可以用于预测的回归模型，但它仍然属于对变量间相关关系的研究范畴。简单回归预测得到的预测值，不是因变量的真实值，是在给定自变量取值下，因变量所有可能取值的期望值。

附stata代码:

use "D:\Desktop\案例分析.dta", clear //导入案例数据scatter y x //做出y和x的相关图cor y x //求出y和x的相关系数，此为相关分析reg y x //将y关于x作回归，得到回归模型，此为回归分析

附案例数据：