香农 通信的数学理论_信息论开山之作——克劳德 E. 香农 1948年 《通信的数学原理》全文【1】...

引言

近来出现了许多以带宽换取信噪比的调制方法，比如 PCM 和 PPM，它们的出现进一步激发了人们对广义通信理论的兴趣。在奈奎斯特（Nyquist）^[1]和哈特莱（Hartley）^[2]发表的一些重要相关论文中，奠定了这一理论的基础。本论文将扩展该理论，增加一些新的因素，具体来说，就是信道中噪声的影响、由于原始消息的统计结构和最终信宿的本质而可能减省的内容。

通信的基本问题就是在一个地方复现在另一个地方选定的消息，这一复现可能是准确的，也可能是近似的。这些消息通常有特定的含义；也就是说，它们会根据某一系统，与特定的物理或概念实体关联在一起。通信的语义与工程问题无关。重要的是：实际消息是从一个消息集合选出的。所设计的系统必须能够处理任意选定的消息，而不是仅能处理实际选择的特定消息，因为在设计系统时，并不知道会实际选择哪条消息。

如果集合中的消息数目是有限的，而且选择每条消息的可能性相等，那就可以用这个消息数或者它的任意单调函数，来度量从集合中选择一条消息所生成的信息量。正如哈特莱所指出的那样，最自然的选择就是对数函数了。如果考虑消息统计信息的影响，如果消息的选取范围是连续的，那必须对其定义进行重要扩展，但在所有情况下，我们使用的度量在实质上都是对数函数。

对数度量之所以更为便利，其原因有多种：

1. 它在实践中更为有用。一些在工程上非常重要的参数，比如时间、带宽、延迟数，等等，往往与可能性的数量的对数值呈线性关系。例如，增加一个继电器会使继电器的可能状态数加倍。如果对这一数目求以 2 为底的对数，则增加一个继电器后，会使结果加 1。使时间加倍，会使可能消息数近似变为原来的平方，而其对数则是加倍，诸如此类。
2. 它更接近于人类对正确度量的直观认知。这一点与第 1 个原因密切相关，因为人们在对实体进行直觉度量时，通常是与公共标准进行线性比较。比如，人们认为，两张打孔卡存储信息的容量应当是一张打孔卡的两倍，两个相同信道的信息传输能力应当是一个信道的两倍。
3. 更适于数学运算。许多极限运算很容易用对数表示，如果采用可能性的数目表示，可能会需要进行冗繁、笨拙的重新表述。

对数底数的选择与信息度量单位的选择相对应。如果所用底数为 2，则所得到的结果可以称为二进制数位（binary digit)，或者简称为 比特（bit），它是由 J. W. Tukey 提议采用的。一个具有两种稳定状态的器件，比如继电器或者触发电路，可以存储 1 比特信息。N 个此种器件可以存储 N 比特，因为可能状态的总数为

，而

。如果所用底数为 10，则所得单位可以称为十进制数字(decimal digit)。因为：

一个十进制数位大约为个

比特。台式计算机上的一个数位轮有 10 个稳定状态，因此，其存储容量是一个十进制数位。在一些涉及积分和微分的分析中，底数

有时会很有用。所得到的信息单位称为自然单位。只需要乘以

就可以将底数 a 改为底数 b。

图1 一般通信系统示意图

我们所说的通信系统，是指图 1 中示意给出的系统类型。它基本上由五部分组成：

1. 信源，生成要传送给接收终端的消息或消息序列。消息可能是各种不同类型：(a) 字符序列，比如电传系统电报机中；(b) 单个时间函数
   ，比如无线电或电话通信中；(c) 时间及其他变量的函数，比如黑白电视机中——这里的消息可以看作是两个空间坐标与时间的函数
   ，也就是摄像管盘面上点
   处在时刻 t 的光强度；(d) 时间的两个或更多个函数，比如
   ——“三维”声传送即属这一情景，如果通信系统要以多工方式为几个独立信道提供服务，则同属这一情景；(e) 几个变量的几个函数——在彩色电视机中，消息包含三个函数
   ，它们都定义在一个三维闭联集(continuum)上——我们还可以将这三个函数看作是定义在该区域上的一个向量场的分量——与此类似，几台黑白电视源所生成的“消息”由许多三变量函数组成；(f) 还会有各种组合情景，比如，在带有关联音频声道的电视中。
2. 发送器，它以某种方式对消息进行处理，生成一个适于在信道中传送的信号。在电话通信中，这一处理就是将声压变换为比例变化的电流。在电报中采用一种编码操作，在信道中生成一系列与消息相对应的点、划和空。在多工 PCM 系统中，必须对不同的语音函数采样进行采样、压缩、量化和编码，最后进行恰当的交错，从而构造出信号。在声码器系统、电视、频率调制中，也都需要对消息进行一些复杂处理才能得到信号。
3. 信道，就是供发送器向接收器传送信号的媒介。它可能是一对导线、一根同轴电缆、一个无线电频带、一道光束，等等。
4. 接收器，通常是执行发送器所做处理的逆处理，由信号重构出消息。
5. 信宿，意欲向其传送消息的人（或物）。

我们希望考虑涉及通信系统的某些一般性问题。为此，首先需要对所涉及的各个物理部分进行抽象，用数学方式表示出来。我们可以将通信系统粗略地分为三大类：离散系统，连续系统，混合系统。离散系统是指其中的消息和信号都是离散符号序列。电报是这种系统的一个典型例子，其中的消息是一个字符序列，信号是一个由点、划和空组成的序列。连续系统是指其中的消息和信号都可以看作连续函数，比如，无线广播或电视。混合系统是指离散变量与连续变量都可能出现的系统，比如语音的 PCM 传送。

我们首先考虑离散情景。这种情景不仅在通信理论中有应用，同样适用于计算机理论、电话交换设计及其他领域。此外，离散情景还为连续情景和混合情景奠定了基础，后两种情景将在本论文的第二部分讨论。

---

第Ⅰ部分：离散无噪声系统

1.离散无噪声信道

电传打字机和电报通讯是信息传送离散信道的两个简单例子。 一般来说，离散信道意味着可以通过一个系统，从一点向另一点传送一个选择序列，而该序列选自一个由基本符号

组成的有限集合。假定每个符号

的特定持续时间为

秒（对于不同的

，此持续时间不一定相同，比如电报中使用的点和划）。并不要求在此系统中能够传送

的所有可能序列；可以仅允许出现特定序列。这些特定序列就是可能出现在该信道中的信号。因此，在电报中，假定这些符号为：(1) 点，先将线路闭合一个时间单位，然后再断开一个时间单位；(2) 划，线路闭合三个时间单位，然后断开一个时间单位；(3) 字符空，比如将线路断开三个时间单位；(4)字空，线路断开六个时间单位。我们可以对允许出现的序列设定限制：不允许两个空相邻（因此，如果两个字符空相邻，则与一个字空相同）。我们现在考虑的问题是，如何度量这样一个信道的信息传输能力。

在电传打字机中，所有符号的持续时间相同，允许出现任何由 32 个符号组成的序列，上面的问题很容易解答。每个符号表示 5 比特信息。如果系统每秒传送 n 个符号，那自然可以说该信道的容量为 5n 比特/秒。这并不是说电传信道总是以这一速度传送信息——这是最大可能速率，后面将会看到，实际速率能否达到这一最大值，取决于向信道馈送信息的信源。

在更一般的情况下，符号的长度不同，而且对允许序列设有限制，我们做出如下定义：

定义：离散信道的容量

给出如下：

式中，

是指在允许出现的信号中，持续时间为

的信号数目。

容易看出，在电传情况下，这一公式简化为前面的结果。可以证明，在人们所关注的大多数情况下，上述极限值存在且有穷。假定允许出现信号

的所有序列，而且这些符号的持续时间为

。信道容量是多少呢？如果

表示持续时间为

的序列数，则有：

该总数等于以

结尾的序列数目之和，这些数目分别为

。由有限差分中一个众所周知的结果可知，对于大的

值

趋近于

，其中

是以下特征方程的最大实数解：

因此，

在对允许出现的序列设定了限制时，仍然能够获得这一类型的差分方程，并由该特征方程求得

。在前面提到的电报情景中，根据最后一个符号或者倒数第二个符号来计算符号序列的数目，可以得出：

因此，

为

，其中

是

的正根。求解此方程后可得

。

在对允许序列设定的限制中，有一种非常普通的类型：假设有大量可能状态

，对于每种状态，只能传送集合中的特定符号

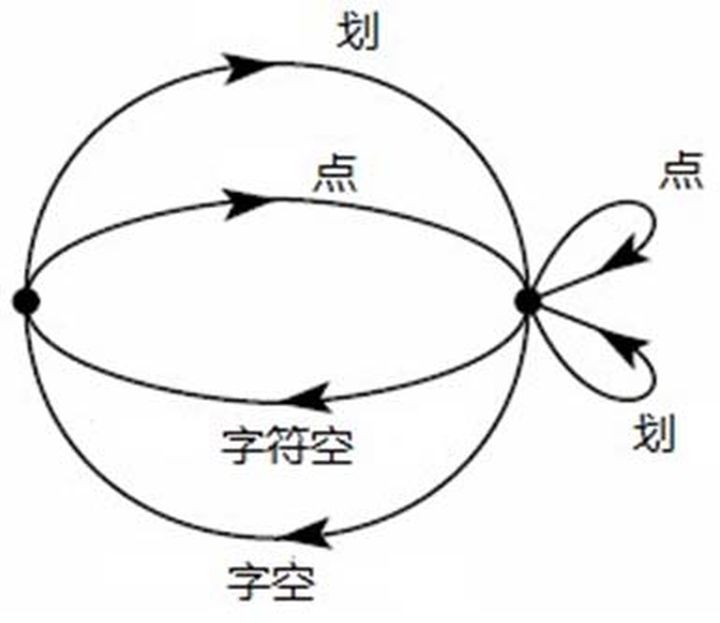
（不同状态对应的子集不同）。在传输一个序列后，系统状态改为一种新的状态，具体取决于原有状态和所传送的特定符号。电报是这种情景的一个简单示例。根据最后传送的符号是不是空格，共存在两种状态。如果是空格，则接下来只能传送一个点或一个划，状态总是发生改变。如果不是空格，则可以传送任意符号，如果发送的是空格，则状态发生变化，如果不是空格，则状态保持不变。这些条件可以用如图 2 所示的线性图表示。交点对应于状态，连线表示一种状态下可以传送的符号及传送符号后所得到的状态。在附录 1 中，如果可以用这种方式来描述对允许序列设定的条件，则

存在，并可计算如下：

定理 1：设

是指在状态

下允许出现并导致状态

的第

个符号的持续时间，则信道容量

等于

，其中

为以下行列式方程的最大实根：

其中，当

时，

，否则，等于 0 。

例如，在电报通讯中（图 2），该行列式为：

展开后，即可得到上文针对这一情景给出的方程。

图2 用图形表示针对电报符号设置的约束条件

2. 离散信源

我们已经看到，在非常一般的条件下，离散信道中可出现信号数的对数随时间线性增加。如果能给出这一增长速率，也就是每秒需要多少比特来表示所使用的特定信号，每秒钟所需要的比特数，就能给出信息传输容量。

我们现在考虑信源。如何用数学描述一个信源呢？一个给定信源每秒生成多少比特的信息呢？问题的要点在于，如何利用信源的相关统计知识，通过信息的正确编码，减少所需要的信道容量。比如，在电报通信中，要传送的消息由字符序列组成。但是，这些序列并不是完全随机的。一般情况下，它们会组成句子，具有某种语言的统计结构，比如英语。字符 E 的出现频率要高于 Q，序列 TH 的出现频率要高于 XP，等等。由于此种结构的存在，我们可以对消息序列进行适当编码，转换为信号序列，以节省时间（或信道容量）。其实在电报通讯中已经进行了一定程度的此种处理：为最常见的英文字母 E 使用最短的信道符号——点；而出现较少的 Q，X，Z 则使用较长的点、划序列来表示。这一思想一直沿用到一个特定的商用编码中，在这些编码中，常见的单词和短语用四字符或五字符代码组表示，大幅缩短了平均时间。现在使用的一些标准问候电报和周年纪念电报扩展了这一思想，将一个或两个句子编码为一个较短的数字序列。

我们可以认为离散信源是逐个字符地生成消息。它将会根据特定概率值选择相继符号，这些概率值通常取决于之前的选择和所考虑的特定符号。如果一个物理系统或者一个系统的数学模型，在一组概率的控制下生成符号序列，则这种系统或模型称为随机过程^[3] 。因此，我们可以考虑用随机过程表示离散信源。相反，任何一个随机过程，只要它生成的离散符号序列是从有限集合中选出的，则可以将其看作离散信源。它将包括类似以下的各种情况：

1. 自然书写的语言，比如英文，德文，中文。
2. 已经用某种量化过程变为离散的连续信源。比如，由 PCM 发送器输出的量化语音，或者是经过量化的电视信号。
3. 数学信源，在此类情况下，我们只是抽象地定义了一个生成符号序列的随机过程。下面是最后一种信源类型的示例。

(A) 假定我们有五个字母 A，B，C，D，E，各字母被选中的概率为 0.2，前后选择之间相互独立。这样会得到一个序列，下面是其中的一个典型示例。

B D C B C E C C C A D C B D D A A E C E E A

A B B D A E E C A C E E B A E E C B C E A D

这一序列是使用一个随机数字表生成的^[4] 。

(B) 使用相同的五个字母，设各概率为 0.4，0.1，0.2，0.2，0.1，连续选择之间互相独立。则由这一信源生成的典型消息为：

A A A C D C B D C E A A D A D A C E D A

E A D C A B E D A D D C E C A A A A A D

(C) 如果相邻符号的选择不是独立的，其概率取决于之前的字符，则会得到一种更为复杂的结构。在最简单的此种类型中，字符的选择仅取决于它前面的一个字母，而与再之前的字母无关。这种统计结构可以由一组转换概率

来描述，该概率是指字母

之后跟有字母

的概率。下标

和

的取值范围为所有可能出现的符号。还有一种等价方式来指定该结构，即给出“连字(digram)”概率

，也就是连字

的相对概率。字母频率

（即字母

的概率）、转换概率

和连字概率

之间的关系由以下公式给出：

作为一个特定示例，假定共有三个字母A，B，C，其概率表为：