分别用经典的能均分定理_分子动力学模拟笔记 —— 经典统计力学基础（2）

1. 热力学极限

热力学极限告诉我们：对于像能量这样随粒子数变化的外延热力学变量（extensive variables），当系统无限大时，其单位粒子或单位体积结果会趋近于一个定值。

证明：

根据切比雪夫不等式，有

代表概率，

、

分别为观测结果

的均值和方差，

为任一常数。如果设变量

为

，带入公式（1）可得

当

时，有

由此可见，系统足够大时，单位变量

会近似等于一期望值

，其在系统中的分布也可近似为以

为中心的delta函数。

---

2. 微正则（NVE）系综（microcanonical ensemble）

弱相互作用（weak interaction）假设

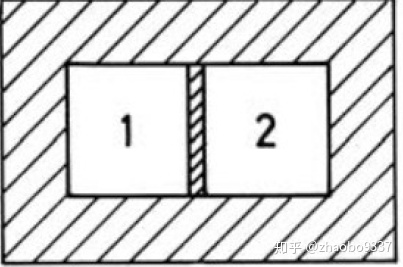
如上图所示，系统中有两个子系统1和2。系统总的哈密顿能量可写成

，

和

分别为子系统1和2的能量，

是两个系统相互作用的能量。在大多数情况下，

相比于

和

可以忽略不计，可近似成

. 这就等同于，

在相空间（phase space）平面中，如果系统1的能量轨迹（trajectory）

已知，系统2可以是能量为

的任一轨迹

。

---

NVE系综的相平均（phase averages）

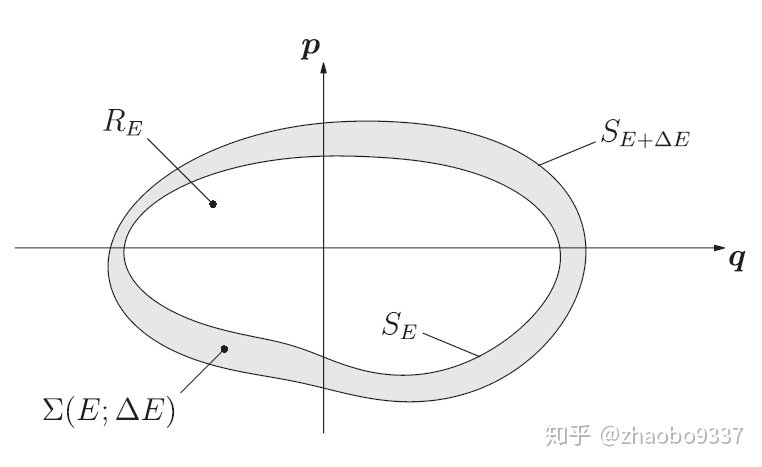
利用相空间（phase space）这样的几何形式便于我们直观地分析孤立的哈密顿体系（微正则系综）。如上图所示依旧是一个相空间（phase space）平面，灰色带状区域表示由

和

两个超平面（hypersurface）围成的能量为

的区间，

。区域体积为

,等同于热力学中的状态数.

是测量精度，相比于

来说非常小。对于粒子数N、体积V和能量E均为常数的孤立系统（NVE系综），超平面内所有状态都是等概率的。

这里我们也采用类似固体物理中描述电子结构的态密度（DOS）的概念，则

可表示为：

其中

为

系统的状态密度，定义为

值得注意的是，

和

随粒子数N呈指数增长

，虽然这里不做证明（感兴趣的话可以自己证一证），但这一结论对后面热力学量的推导非常重要。

我们定义一个在区间

内为常数，外部为零的分布函数

，相空间坐标系

由一个坐标

表示，

满足：

也满足归一性条件，即

结合公式（4），（6）和（7）可得

因此，该孤立系统中函数

的平均值（phase average）可表示为：

当函数

或为任意常数时，可以得到态密度

. 在考虑量子力学的情况下，平均值修正为：

其中

是普朗克常数，

是粒子数，

项是考虑了粒子的不可分辨性（indistinguishable）.

内能、温度和熵

在一般热力学平衡情况下，内能等于哈密顿量的平均值

在像微正则系综这样的封闭孤立系统中，哈密顿量是一个常数，即

，所以有

在非微正则系综如正则系综（canonical ensemble）中，公式（10）依然成立，但是

会在

附近上下波动，即

.

现在，我们假设有两个子系统

和

，初始能量分别为

和

，接着让这两个子系统相互接触，在这个过程中系统的总能量保持不变，

.在这里我们考虑了前面提到的弱相互作用近似，因此总能量可以写成两个系统的能量和。

我们想要试图寻找的是最终到达平衡状态时系统

和

的能量，

和

. 有两个条件可以用来判定系统到达平衡：两个子系统温度相同或当系统熵为最大值。

在平衡态有如下关系：

和

分别为

，

系统的熵。那么公式（12）如何和微观粒子的统计学联系起来呢？

从宏观上看，平衡态相当于系统熵达最大值；从热力学统计学角度考虑，平衡态对应于系统所有状态中概率最大的的某个状态。设系统

能量为

的概率为

，以相空间（phase space）为模型，

可以用系统

的体积

，

的体积

和总体积

表示：

的最大值对应于

，因此由公式（13）可得：

两边同除

并换成对数形式可得

对比公式（11），（12）和（15），可得到

，比例系数就是 玻尔兹曼常数

.

因此熵

可以表示为（含量子力学修正）

：

熵也可以用态密度（DOS）表示为

在相空间中，

在粒子数很大时可以近似成一常数，利用前面

和

随着粒子数N呈指数增长这一结论，公式（17）最右边等式的第二项可以忽略，

从而得到由相空间体积和态密度表示的熵

宏观变量温度也可以由相空间变量表示为

---

维里方程（virial theorem）和均分（equipartition）方程

NVE系综的均分定理（equipartition theorem）可由下式表示：

其中

和

可以是动量

或位置

的任意一个，

是Kronecker delta函数（

时，

；否则

）。

通过公式（20）我们可以快速得到系统的热力学变量值。

当

为动量时

，可以得到一下关系：

令

且应用哈密顿公式，

由此可以得到，系统平衡时每个自由度的动能均为

. 在MD模拟中我们通过该关系由瞬时动能计算瞬时温度。对

个自由度求和：

利用公式（24）可以得到温度地表达式为

是系统的振动（vibrational）动能。

当

为位置自由度时

，又可以得到如下关系

一个原子自由度为

，因此公式（26）对单一原子求和可得：

其中

为作用在原子

上的合力。把所有原子加起来，可以得到

式中第一项的

叫做这个系统的维里量（virial）

. 结合公式（24）可以得到系统动能和维里量之间的关系为

运用维里量我们可以进一步得到系统压力（pressure）的表达式。首先，维里量可以分为与系统内力关联的内部项（internal part）以及和外力关联的外部项（external part）。我们假设把一个系统封闭在一个箱子里，内力是原子间的相互作用力，而外力来自于外界对箱子表面的压力。关于维里量外部项的均分（equipartition）方程可表示为

考虑系统为理想气体（ideal gas）的情况，内力为零，则维里量内部项为零，结合公式（28）和（30）可得大家熟悉的理想气体状态方程

对于非理想气体，则有

为维里量内部项。

上面推导的均分定理（equipartition theorem）和维里定理（virial theorem）不仅适用于微正则系统，也适用于其他几个系综。但是均分定理仅限于经典力学的范畴，对于能量量子化的量子力学体系不再适用。比如，通过均分定律我们预测晶体的热熔是与温度无关的量（Dulong-Petit law），但实验已经证明，在低温下热熔随温度的下降而减小，在0K时可以减小到0。

参考书目：Tadmor, E., & Miller, R. (2011). Modeling Materials: Continuum, Atomistic and Multiscale Techniques. Cambridge: Cambridge University Press.