fmod实现声音波形_【脑洞向】用物理方法穷尽一切声响，编写一部“终极声音字典”！...

今天突然开了这个脑洞，下面对这个脑洞谈谈个人的看法，以此抛砖引玉。

我假想了一种理论模型，姑且命名为“终极声音字典”——它遍历了自然界所有声响的一切可能性。假设它存在，那么，打开任一段声音 / 音频文件（可以是世界上任何一首音乐、任何一段语音、自然界各种发出的声响……）等等，都可以在这个理论模型中找到它的“出处”。这个理论模型存在吗？如果存在，用何种方法实现？

从傅立叶理论，任何声音都可以分解为纯音（正弦波）的叠加。一个任意的有限长度的声音，数字化后都可以写成这样的函数形式：

（可简写为：

）

或：

（可简写为：

）

其中，

代表直流偏移，后面每个正弦项的系数

和余弦项的系数

（或：振幅系数

和相位

）塑造了这段周期性声音信号的特征。

那么，我们就可以用类似“音集”的方式表示一个周期性声音波形。例如下面这个波形：

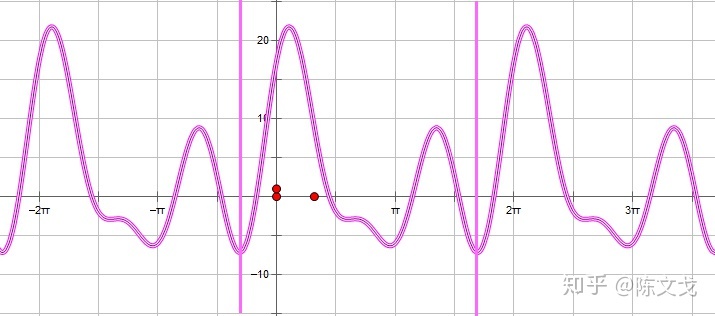
（中间的竖线间隔该波形的周期。）当这个函数的项数越来越多，波形就越来越复杂，周期也越来越长。傅立叶级数是一个无穷级数，也就是说，世界上任何一段音频都可以用这个级数来逼近，只要项数足够多。

用在二维平面上，就像是这个例子：“川普曲线”——和它的解析式。

可见，用这个级数，只要解析式的项数足够多，任何图形都可以画出来。

回到上面举的波形：

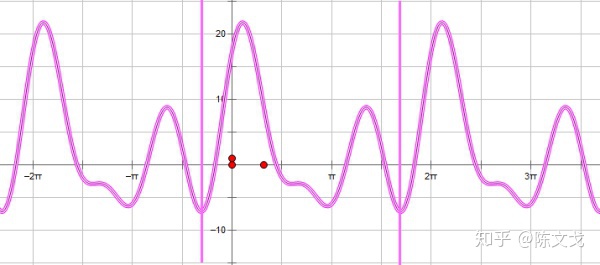
它的解析式是：

这个式子，我们就“提取”出当中的各项系数，用“音集”的方式写成：

这就为声音波形建立了“音集”，一个特征的波形只会对应唯一的“音集”。

（关于“音集”理论，可以参考此文：小议如何将音集理论推广至所有微分音以至于频谱音乐）

然而，傅立叶级数是一个无穷级数，也意味着如果要遍历所有声音，项数将趋于无穷，这是不可能的。

但是即使如此，仍然有希望：例如，一段采样率为44100Hz的音频（CD音质）在人耳听觉已经没什么失真。因此，在未来，我们也许可以如此遍历一切声响，把一切声响记录为：

的形式，从而完成这部“终极声音辞典”的构建。