π型滤波频率计算_【每日电路赏析】滤波电路

滤波器在功率和音频电子中常用于滤除不必要的频率。而电路设计中，基于不同应用有着许多不同种类的滤波器，但它们的基本理念都是一致的，那就是移除不必要的信号。所有滤波器都可以被分为两类，有源滤波器和无源滤波器。有源滤波器用到1个或多个有源器件和其它无源器件组成，而无源滤波器则只有无源器件组成。本文中，我们向大家介绍其中的π滤波器，它在电源电路设计中非常适用。π滤波器π滤波器是无源滤波器，是由3个器件组成，而非传统的两器件组成的无源滤波器。它的结构有点像希腊字母π，所以因此得名π滤波器。π滤波器用于低通滤波π滤波器是一种出色的低通滤波器，与传统的LC滤波器有很大不同。当π滤波器用于低通滤波时，输出稳定且K值固定。使用π滤波器实现的低通滤波器很简单。π滤波器电路由两个电容并联，再与一个电感串联组成如下的π形状的电路。如上图所示，两个电容接地的同时中间与一个电感串联。因为这是一个低通滤波器，它在高频下产生高阻抗，在低频下产生低阻抗。因此，常用于传输线路中隔绝不必要的高频信号。π滤波器中每个元件的值的计算可以由以下公式得出，方便你设计应用。截止频率fc=/1/ᴫ(LC)1/2电容值 C=1/Z0 ᴫfc电感值 L1=Z0/ ᴫfc其中Z0为阻抗π滤波器用于高通滤波π滤波器同样可以被配置成高通滤波器。这种配置下，滤波器会隔绝低频信号，通过高频信号。而且同样由两种无源器件组成，两个电感和一个电容。在高通滤波下，π滤波器电路的组合方式有些不同，具体如下图。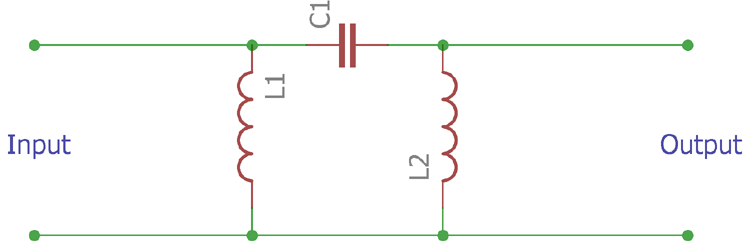在该配置下，其参数计算参照以下公式。截止频率 fc= 1/4ᴫ(LC)1/2电容值 C=1/4Z0ᴫfc阻抗值 L1=Z0/4ᴫfcπ滤波器的优点高输出电压π滤波器的输出电压很高，所以适用于需要高压直流滤波的应用。低纹波系数若以低通滤波配置来进行直流滤波的话，π滤波器是一种效率很高的滤波器，可以从桥式整流器输出端滤除不必要的交流纹波。电容在交流下阻抗低，但在直流下阻抗高。在RF应用中设计方便在控制中的RF环境中，需要更高频率的传输，比如GHz级别的宽带，高频π滤波器在PCB中更容易设计。高频π滤波器还会提供比其它半导体滤波器更强大的脉冲免疫。π滤波器的缺点电感上的电压值升高与射频设计不同，从π滤波器输出的大电流是不恰当的，因为这股电流必须流经电感。如果负载电流很大的话，那么电感上的电压也会随之变大，这样就需求更加笨重和昂贵的电感。同样，电感上的大电流会致使能量耗散，从而降低效率。大输入电容π滤波器的另一个问题就是输入电容的值很大。π滤波器输入端需要高容值在一些空间受限的应用中成了挑战。同时大电容同样提高了设计的成本。糟糕的电压调节π滤波器不适用于负载电流不稳定且一直在变化的应用。当负载电流变化大的时候，π滤波器的电压调节很糟糕。这样的应用中更适合L型滤波器。π滤波器设计的经验在电子电力设计中：

• π滤波器的layout需要较宽的走线

• 将π滤波器与供电元件隔离开来尤为重要

• 输入电容，电感和输出电容的间距要小

• 输出电容的地线层需要直接与驱动电路相连

在射频电路中：

• RF应用中元器件的选择非常关键。尤其是要注意元器件的精度。

• PCB走线的增加会在电路中产生电感。所以电感取值时要考虑到PCB走线的电感。应该用合理的方式来减少杂散电感。

• 尽可能减少杂散电容。

• 元件布局要尽可能紧密。

• 射频应用中的输入与输出适合使用同轴电缆。