本文介绍了基于Motifs的频谱聚类方法，详细阐述了图分区的三个阶段：预处理、分解和分组。通过分析邻接矩阵、拉普拉斯矩阵及其特征向量，探讨了如何利用特征向量进行低维表示并进行聚类。文章还讨论了如何选择最佳的K值，并提出了高阶分区问题，特别是如何在加权图上应用频谱聚类来发现低基序传导率的簇。此外，展示了该方法在食物链网络和基因调控网络中的应用案例。
- 三个基本阶段：
- 1)预处理
- 构造图形的矩阵表示
- 2)分解
- 计算矩阵的特征值和特征向量
- 根据一个或多个特征向量将每个点映射到一个较低维的表示形式
- 3)分组
- 根据新的表示法将点分配给两个或多个群集
- 1)预处理
- 首先，让我们定义问题
图分区
- 无向图G(V，E)
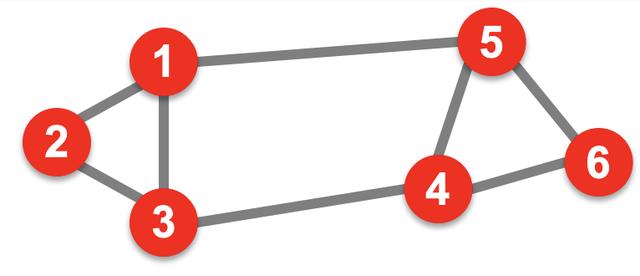
- 双分区任务
- 把顶点分为两个不相连的组A，B
- 问题
- 如果确定分区是“好”的？
- 如何找到这两个组？
- 什么是一个好的分区？
- 最大化组内连接的数量
- 最小化组间连接的数量
图切割
- 根据分区的“切边”来表达分区目标
- 切割：每组中有一个端点的一组边：
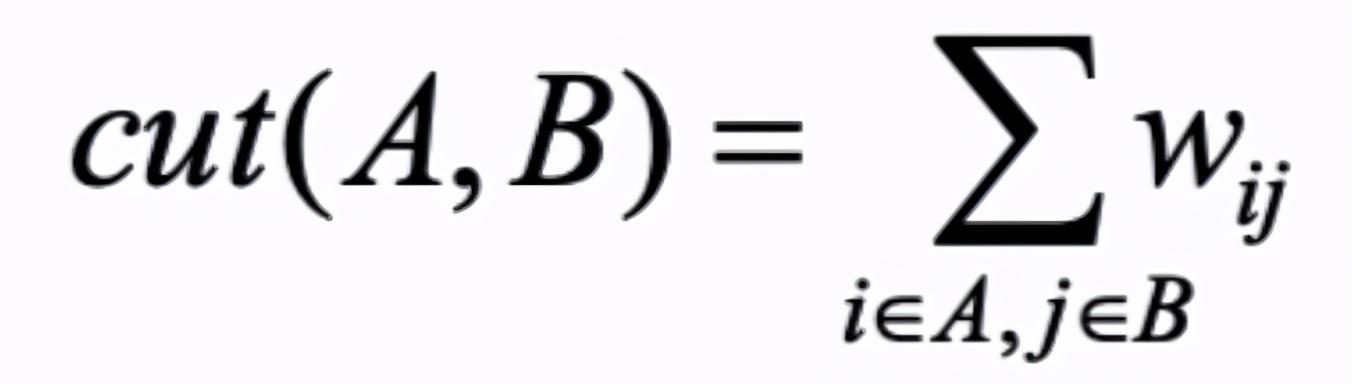
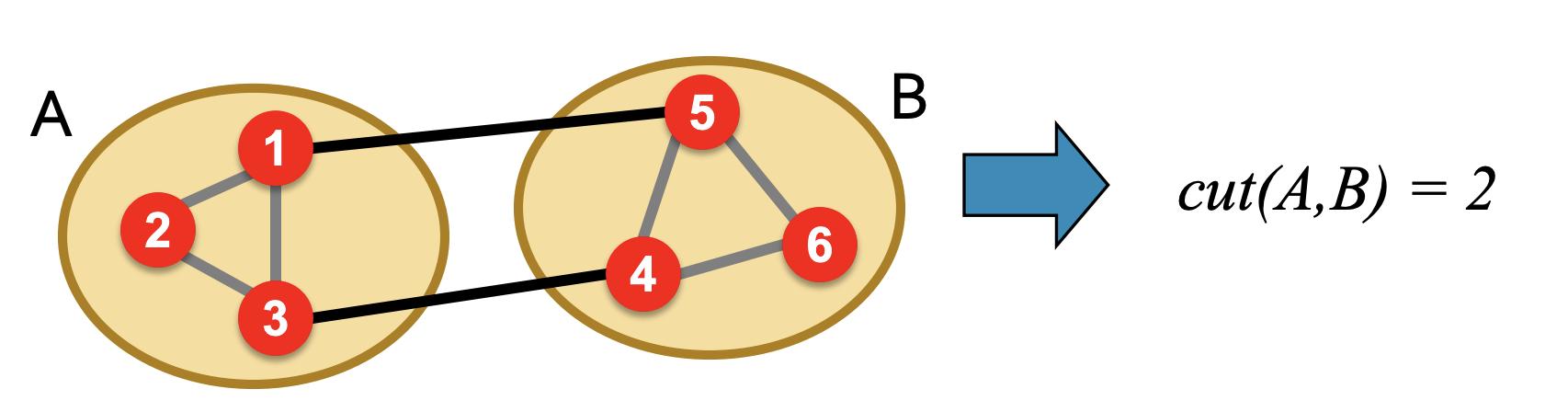
- 标准：最低限度
- 最小化组间连接的权重
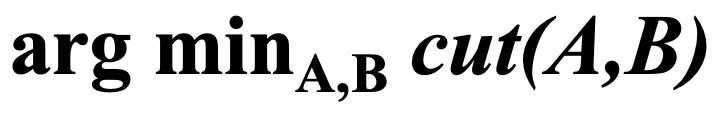
退化：
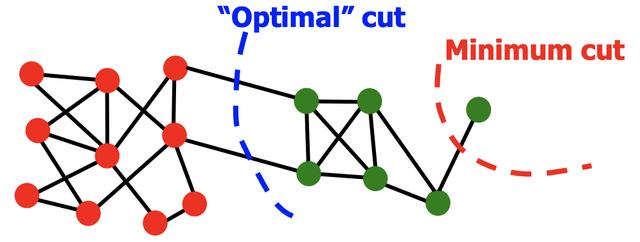
- 问题：
- 仅考虑外部群集连接
- 不考虑内部集群连接
- 判据：导电率 [Shi-Malik，’97]
- 相对于每个组的密度，组之间的连通性
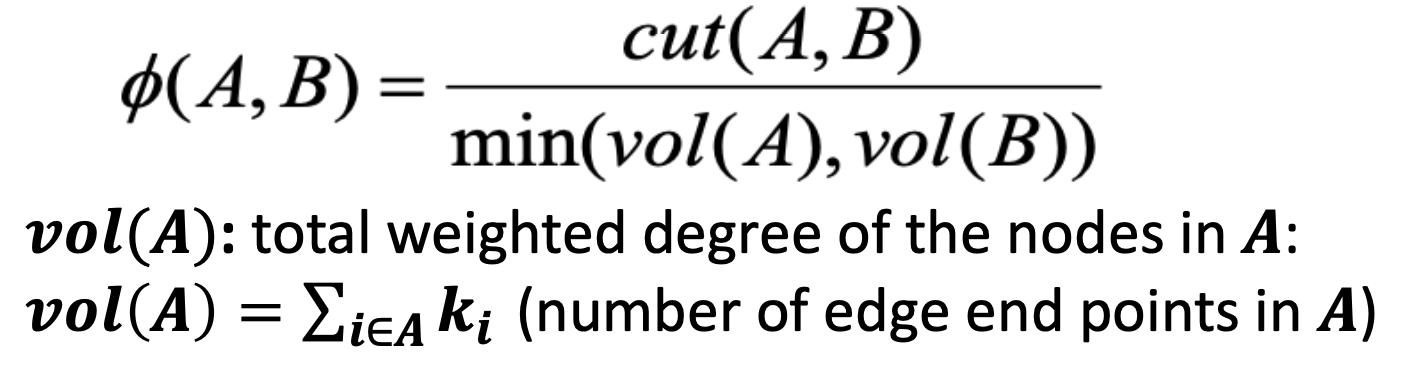
- 为什么使用这个标准？
- 产生更均衡的分区
- 我们如何有效地找到一个好的分区？
- 问题：计算最佳电导率切分是NP-Hard问题
频谱图分区
- A：无向G的邻接矩阵
- Aij = 1(i，j)是边，否则为0
- x是Rn中的向量，具有分量(x1，…，xn)
- 将其视为G每个节点的标签/值
- Ax 是什么意思？
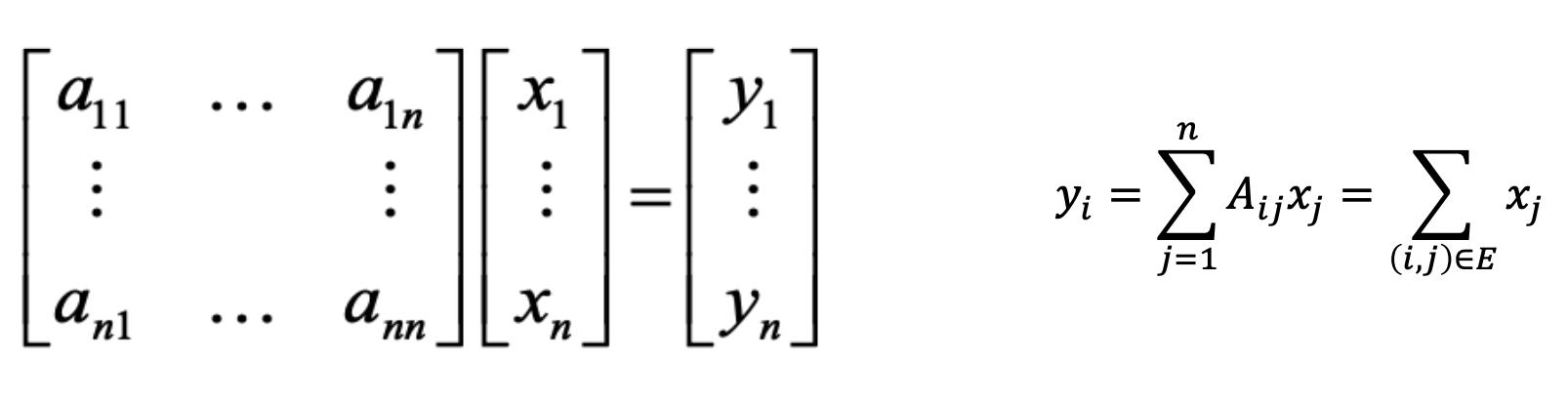
- 项yi是i的邻居的标签xj的总和
- Ax的第j个坐标：
- j的邻居的x值之和
最低0.47元/天 解锁文章
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
