c语言编写walshall算法,Warshall算法求传递闭包及Python编程的实现

弗洛伊德算法-Floyd(Floyd-Warshall)-求多源最短路径，求传递闭包

Floyd算法又称为插点法，是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法，

与Dijkstra算法类似。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。

为什么要求传递闭包？

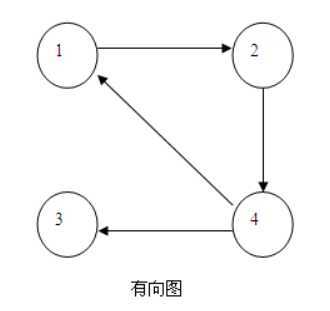
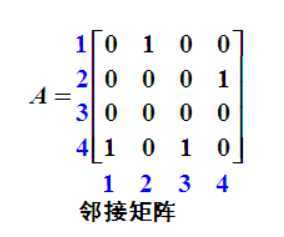
因为：一个有n个顶点的有向图的传递闭包为：有向图中的初始路径可达情况可以参见其邻接矩阵A，

邻接矩阵中A[i,j]表示i到j是否直接可达，若直接可达，则A[i,j]记为1，否则记为0；两个有向图

中i到j有路径表示从i点开始经过其他点(或者不经过其他点)能够到达j点，如果i到j有路径，

则将T[i,j]设置为1，否则设置为0；有向图的传递闭包表示从邻接矩阵A出发，求的所有节点

间的路径可达情况，该矩阵就为所要求的传递闭包矩阵

warshall传递闭包算法的目的：就是由邻接矩阵出发，进行探索求出最终的传递闭包

(i是行，j是列)

算法过程：

(1)i=1时，第一列有A[4，1]=1，将第四行元素分别与第一行对应元素进行

逻辑加(或运算)：

0  1  0  0

0  0  0