层次聚类算法C++实现与数据挖掘项目实践

本文还有配套的精品资源，点击获取

简介：层次聚类算法是一种重要的数据挖掘无监督学习方法，它通过分析数据集的内在结构来对相似数据进行分组。本项目旨在使用C++语言实现层次聚类算法，并通过分析Iris数据集来实践算法。Iris数据集包含鸢尾花的四个特征，适用于三种鸢尾花品种的分类。项目中将介绍算法的两种主要类型：凝聚型和分裂型，并详细阐述了实现的关键步骤，如距离计算、构建距离矩阵、簇的构建、剪枝条件、结果保存和可视化。通过项目实践，你将深入理解层次聚类算法的工作原理，并提升C++编程技能，特别是在数据处理和算法实现方面。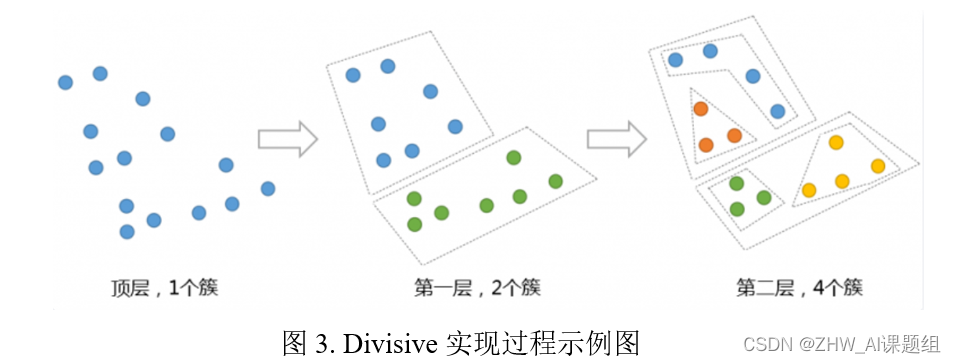

1. 层次聚类算法概念

层次聚类算法是一种无监督的机器学习方法，它通过构建一个聚类的层次结构（即树状图），来发现数据中隐含的模式或分组。该方法不需要预先设定簇的数量，它通过计算样本点或簇之间的距离，逐步合并或分裂簇，直至满足终止条件。层次聚类可以细分为凝聚型（Agglomerative）和分裂型（Divisive）聚类，其中凝聚型从每个样本点为一个簇开始，逐步合并，而分裂型则从一个包含所有样本点的簇开始，逐步分裂。

层次聚类的核心优势在于其直观性和灵活性，能够提供一个包含数据所有可能分层的全局视图。然而，它在处理大规模数据集时可能会遇到计算和存储的挑战，因为其时间复杂度和空间复杂度较高，特别是对于距离矩阵的处理。

2. 数据挖掘中的层次聚类应用

2.1 层次聚类在数据挖掘中的角色

2.1.1 数据挖掘的基本流程

数据挖掘是一系列分析大量数据以发现有价值信息和知识的过程。它结合了统计学、机器学习、数据库技术以及人工智能等领域的知识。数据挖掘过程可以分为几个阶段：

1. 问题定义 ：明确业务目标和需求，确定数据挖掘的具体目的。
2. 数据采集 ：从各种数据源中收集所需的数据。
3. 数据预处理 ：包括数据清洗、数据转换、数据集成和数据归约等，为分析准备质量高的数据集。
4. 数据探索 ：通过可视化和统计分析对数据进行初步探索。
5. 构建模型 ：选择适合的算法，根据数据特征建立预测模型。
6. 评估与解释 ：评估模型的效果，对结果进行解释，确认发现的知识。
7. 部署 ：将模型部署到生产环境中，实施决策。

2.1.2 聚类分析在数据挖掘中的重要性

聚类分析是数据挖掘中的一种基本分析方法，其目的是将数据集中相似的对象分组。聚类分析不依赖于预先标记的数据，属于无监督学习的范畴。它在数据挖掘中的重要性体现在以下几点：

1. 数据理解 ：聚类可以揭示数据的内在结构，帮助理解数据的分布情况。
2. 数据简化 ：将复杂的数据集简化为小的、可管理的组，便于进一步分析和决策。
3. 异常检测 ：异常点往往会在聚类过程中被自然分隔开来，从而能够被检测。
4. 特征提取 ：通过聚类可以提取代表性的特征或元数据。
5. 子群分析 ：在特定子集中发现具有共同特征的群体，这在市场细分和客户关系管理中尤为重要。

2.2 层次聚类算法的优势与局限性

2.2.1 层次聚类算法的优势

层次聚类算法通过构建一个层次的嵌套簇结构来展示数据的聚类情况。它具有以下优势：

1. 无需指定簇的数量 ：层次聚类不依赖于事先指定簇的数量，这避免了在K-means算法中必须猜测最佳簇数的问题。
2. 树状结构 ：通过树状图（Dendrogram）可以清晰地看到数据对象是如何聚合的，有助于理解数据的层次结构。
3. 灵活性 ：可以通过剪枝操作，根据不同的需求提取不同层次的聚类结果。
4. 无中心点依赖 ：与基于中心点的聚类方法不同，层次聚类不依赖于簇中心点的初始选择。

2.2.2 层次聚类算法的局限性

尽管层次聚类有许多优势，但它也有一些局限性：

1. 计算复杂度高 ：大规模数据集上的计算时间通常很长，尤其是凝聚层次聚类方法。
2. 不稳定性 ：当数据集有噪声或离群点时，层次聚类可能产生不稳定的结果。
3. 内存消耗大 ：在构建距离矩阵时需要大量的内存空间，这在处理大型数据集时可能会成为瓶颈。
4. 距离度量选择敏感 ：聚类结果对所选用的距离度量方法很敏感，可能需要专业知识来选择恰当的距离度量。

层次聚类算法的这些优势和局限性使其在数据挖掘的许多应用中成为了一个有力的工具，尽管它并不总是最佳选择，特别是在处理非常大的数据集时。在下一节中，我们将探讨如何使用C++实现层次聚类算法，以及其具体的编程实现细节。

3. C++语言实现层次聚类

3.1 C++编程基础

3.1.1 C++语言特性简介

C++ 是一种静态类型、编译式、通用的编程语言，它支持过程化编程、面向对象编程和泛型编程。C++ 继承了 C 语言高效、灵活、表达力强的特点，并在此基础上增加了面向对象编程的特性，如类和对象、继承、多态等。此外，C++ 还支持模板编程，这使得代码复用性更高，能够创建更加通用的数据结构和算法。

C++ 提供了丰富的库，包括STL（标准模板库），它包含了一系列数据结构如向量、列表、集合等，以及算法如排序和搜索等，极大地方便了数据处理和操作。由于其接近硬件层面的性能，C++ 常用于系统软件开发，如操作系统、游戏引擎等，同时在科学计算、数值分析等数据密集型领域也有广泛应用。

3.1.2 开发环境搭建

开发C++项目，首先需要安装一个C++编译器。最常用的编译器包括GCC（GNU Compiler Collection）、Clang和MSVC。GCC和Clang适用于Linux和macOS系统，MSVC是Windows平台上的编译器。集成开发环境（IDE）提供了代码编辑、编译、调试等一体化功能，常用的IDE有Visual Studio（Windows）、Xcode（macOS）以及跨平台的CLion、Eclipse CDT等。

搭建C++开发环境时，需要下载并安装所选的IDE和相应的编译器。例如，在Windows系统上，推荐使用Visual Studio，它内置了最新版本的MSVC编译器。在安装过程中，确保选择安装C++开发环境的相关组件，如Visual C++组件。

3.2 C++实现层次聚类算法

3.2.1 算法核心代码解析

层次聚类算法的核心在于递归地合并或拆分簇，直到满足特定的终止条件。在C++中实现层次聚类算法，需要定义数据结构来存储对象以及它们之间的相似性或距离，以及算法逻辑来构建层次结构。

下面是一个简化的C++代码示例，它展示了如何计算对象之间的距离并存储在矩阵中，这是层次聚类算法的核心步骤之一。

#include <iostream>
#include <vector>
#include <cmath>

using namespace std;

// 计算两个向量之间的欧氏距离
double euclideanDistance(const vector<double>& v1, const vector<double>& v2) {
    double sum = 0.0;
    for (size_t i = 0; i < v1.size(); ++i) {
        sum += pow(v1[i] - v2[i], 2);
    }
    return sqrt(sum);
}

int main() {
    // 示例数据集，每一行代表一个数据点
    vector<vector<double>> dataset = {
        {1.0, 2.0},
        {2.0, 3.0},
        {4.0, 5.0},
        {5.0, 6.0}
    };

    // 计算距离矩阵
    vector<vector<double>> distanceMatrix(dataset.size(), vector<double>(dataset.size()));

    for (size_t i = 0; i < dataset.size(); ++i) {
        for (size_t j = i; j < dataset.size(); ++j) {
            double dist = euclideanDistance(dataset[i], dataset[j]);
            distanceMatrix[i][j] = dist;
            distanceMatrix[j][i] = dist; // 距离矩阵是对称的
        }
    }

    // 打印距离矩阵
    for (const auto& row : distanceMatrix) {
        for (const auto& val : row) {
            cout << val << " ";
        }
        cout << endl;
    }

    return 0;
}

在上述代码中，我们定义了一个计算欧氏距离的函数 euclideanDistance ，它接受两个浮点数向量作为参数，并返回它们之间的欧氏距离。在 main 函数中，我们创建了一个简单的数据集并计算了它们之间的距离矩阵。距离矩阵是一个二维向量，其中 distanceMatrix[i][j] 存储了数据集中第 i 个和第 j 个点之间的距离。

3.2.2 C++与数据结构的选择

在实现层次聚类算法时，数据结构的选择至关重要。通常，需要一个有效的方式来存储对象、它们的特征以及对象之间的相似性或距离。在C++中，可以根据需要选择不同的数据结构来优化性能和资源使用。

对于存储数据集，可以使用 std::vector<std::vector<double>> 来存储多维数据点。对于距离矩阵，可以选择使用 std::vector<std::vector<double>> 或者 std::map<std::pair<int, int>, double> ，其中后者更适合动态添加距离数据且不占用过多内存空间。

选择数据结构时还应考虑以下因素：

• 内存占用 ：选择能够最小化内存占用的数据结构。
• 访问效率 ：确保数据结构支持高效的读写操作。
• 扩展性 ：如果数据集大小可变，选择能够动态调整大小的数据结构。

在层次聚类算法中，通常需要频繁访问和更新距离矩阵，因此数据结构的选择需要平衡内存使用和访问效率。例如，对于大型数据集，使用稀疏矩阵来存储距离矩阵可能是更好的选择，这样可以避免存储不必要的距离值。

层次聚类算法的实现细节会根据具体的应用场景和数据集特点有所不同。在设计算法时，应充分考虑数据结构的选择，以及如何通过这些数据结构高效地实现层次聚类的核心逻辑。

4. Iris数据集与层次聚类分析

4.1 Iris数据集概述

4.1.1 数据集来源与特点

Iris数据集是由英国统计学家和生物学家Ronald Fisher在1936年整理并发表的。该数据集旨在对鸢尾花（Iris）植物的三个不同种类进行分类，即Setosa、Versicolour和Virginica。数据集包含了150个样本，每个样本有四个属性：萼片长度、萼片宽度、花瓣长度和花瓣宽度，所有属性的度量单位为厘米。

Iris数据集以其清晰的分类标签和较少的维度而著名，在机器学习和数据分析领域中常用作聚类算法和分类算法的测试数据。它的特点是数据量适中，数据结构简单明了，而且各属性间的差异性较为明显，便于直观地展示聚类分析的效果。

4.1.2 数据预处理步骤

在进行层次聚类之前，数据预处理是必不可少的步骤。以下是Iris数据集预处理的几个主要步骤：

1. 数据清洗 ：检查数据集中是否有缺失值或异常值。Iris数据集通常不含有缺失值，但若数据集中存在，应采取相应措施进行处理，比如插值填补或者删除。

2. 标准化处理 ：由于每个属性的量纲不同，直接用于聚类可能会造成某一维度占主导的情况。为消除量纲的影响，常用的方法包括最小-最大标准化和Z-score标准化。在这个数据集上，通常采取最小-最大标准化方法。

3. 特征选择 ：虽然Iris数据集只有四个特征，但理论上还是需要判断哪些特征对聚类最有效。在实际应用中，可以采用主成分分析（PCA）等方法减少特征维度。

4.2 Iris数据集的层次聚类实施

4.2.1 层次聚类流程详解

层次聚类的核心思想是将数据点或已经形成的簇按某种规则逐步合并，形成一个层次的嵌套结构。具体实施步骤可以分为以下几个阶段：

1. 计算距离矩阵 ：首先，我们需要计算数据集中所有样本间的距离，构建一个距离矩阵。在Iris数据集中，我们通常使用欧氏距离来衡量样本间的相似度。

2. 初始化簇 ：每个数据点在开始时各自作为单独的一个簇。

3. 合并簇 ：根据距离矩阵中最小的距离合并两个最近的簇，并更新距离矩阵。

4. 重复合并 ：重复上一步骤，每次合并最小距离的簇，直到满足聚类结束条件，例如达到预定的簇数目。

4.2.2 结果解释与分析

通过层次聚类算法分析Iris数据集后，我们可以得到一个树状图（Dendrogram），该图展示了聚类的层次结构。通过观察树状图，我们可以确定最佳的簇数目以及每个数据点的归属。

为了更直观地展示聚类结果，可以采用绘制散点图的方式。在二维或三维散点图中，我们可以按照聚类结果标记不同颜色的点，从而直观地看出聚类的效果。

接下来是一个使用Python语言和scikit-learn库进行层次聚类的示例代码，包括数据预处理、距离矩阵计算和聚类分析的全过程：

import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.preprocessing import MinMaxScaler
from sklearn.cluster import AgglomerativeClustering
import matplotlib.pyplot as plt
from scipy.cluster.hierarchy import dendrogram, linkage

# 加载数据集
iris = load_iris()
X = iris.data

# 数据标准化
scaler = MinMaxScaler()
X_scaled = scaler.fit_transform(X)

# 计算距离矩阵
Z = linkage(X_scaled, method='ward')

# 绘制Dendrogram
plt.figure(figsize=(10, 7))
plt.title('Hierarchical Clustering Dendrogram')
dendrogram(Z, labels=iris.target_names, leaf_rotation=90)
plt.show()

# 层次聚类
cluster = AgglomerativeClustering(n_clusters=None, distance_threshold=0, linkage='ward')
cluster.fit(X_scaled)

# 将聚类结果添加到原始数据中
iris_df = pd.DataFrame(X_scaled, columns=iris.feature_names)
iris_df['cluster'] = cluster.labels_

# 查看聚类结果
print(iris_df.groupby('cluster').mean())

在上述代码中，首先导入了必要的库和Iris数据集，然后进行了数据的标准化处理。接着，使用 linkage 函数计算了数据的距离矩阵，并通过 dendrogram 函数绘制了聚类的树状图。最后，使用 AgglomerativeClustering 类实现了层次聚类，并将聚类结果添加到原始数据中以进行进一步分析。

通过观察聚类结果和散点图，可以对聚类效果进行初步的评估。例如，若发现聚类结果与真实标签有较大的差异，则可能需要重新选择特征或者调整层次聚类的参数，比如距离计算方法或合并规则等。

5. 距离计算与聚类策略

距离计算是层次聚类算法中最为核心的部分，它决定了数据点之间的相似度或者差异度。而聚类策略则直接影响到最终形成的簇的质量与数量。本章将详细介绍距离计算的不同方法，距离矩阵的构建过程，以及不同的聚类策略和剪枝条件的设定。我们还将探讨如何进行结果的可视化展示。

5.1 距离计算方法详解

距离计算是评估两个数据点之间相似度的基础。在聚类算法中，距离度量的选择可能会直接影响到最终的聚类结果。下面我们将介绍两种最常见的距离计算方法。

5.1.1 欧氏距离的定义与应用

欧氏距离是最直观的距离度量方法，它描述的是在欧几里得空间中两点间的直线距离。其数学定义如下：

[ d(p, q) = \sqrt{\sum_{i=1}^{n}(q_i - p_i)^2} ]

其中，( p ) 和 ( q ) 是两个 n 维空间中的点，( d(p, q) ) 表示两点间的欧氏距离。在实际应用中，欧氏距离是最常用的度量方式，尤其是在没有先验知识的情况下。例如，在图像识别、传感器数据处理等领域中，欧氏距离可以提供直观且有效的相似度评估。

5.1.2 曼哈顿距离的定义与应用

曼哈顿距离又称为城市街区距离，它测量的是在标准坐标系上的点沿着轴线的绝对轴距总和。其数学定义为：

[ d(p, q) = \sum_{i=1}^{n}|q_i - p_i| ]

其中，( p ) 和 ( q ) 的定义与欧氏距离相同。与欧氏距离不同的是，曼哈顿距离不考虑空间中的对角线距离，而是只考虑各个维度上数值的绝对差之和。在曼哈顿距离适用于那些每个维度都是独立的情况，比如在网格状的城市街道规划中，两点间的实际行驶距离就是曼哈顿距离。

5.2 距离矩阵与簇构建策略

距离矩阵是层次聚类的基础。簇构建策略则依赖于距离矩阵来决定数据点如何被聚集成簇。下面我们将讨论这些概念。

5.2.1 距离矩阵的构建过程

距离矩阵是一个二维数组，它记录了数据集中每对点之间的距离。构建距离矩阵的过程通常如下：

1. 初始化一个空的距离矩阵 ( M )，大小为 ( n \times n )，其中 ( n ) 是数据点的数量。
2. 遍历数据点对，使用所选的距离度量方法计算每对点之间的距离。
3. 将计算得到的距离值填入矩阵的对应位置。

构建距离矩阵是一个计算密集型的过程，其复杂度为 ( O(n^2) )。对于大型数据集，这可能成为性能瓶颈。

5.2.2 凝聚型与分裂型聚类策略比较

层次聚类算法有两种主要的簇构建策略：凝聚型（自底向上）和分裂型（自顶向下）。

• 凝聚型层次聚类 （Agglomerative Hierarchical Clustering）：初始时，每个数据点被视为一个独立的簇。接着，算法反复地合并最相似的簇，直到达到预定的簇数量或满足停止条件。凝聚型方法更容易实现，且通常对大数据集更有效率。

• 分裂型层次聚类 （Divisive Hierarchical Clustering）：与凝聚型相反，分裂型层次聚类从一个包含所有点的簇开始，然后逐步分裂，直到每个点自成一簇或达到其他停止条件。分裂型方法通常比凝聚型算法复杂，但可以更灵活地处理大型数据集。

5.3 剪枝条件与结果可视化

剪枝条件是控制聚类结果的重要参数，而结果可视化则是理解和解释聚类结果的有效手段。

5.3.1 剪枝条件的设定与优化

剪枝条件用于确定何时停止聚类过程。它可能基于以下几种方式：

• 距离阈值 ：当两个簇之间的距离超过特定阈值时，停止聚类。
• 簇大小 ：当簇中的数据点数量小于某个数值时，停止聚类。
• 簇的均匀性 ：例如，当簇内的方差小于某个值时，认为簇内数据足够相似，可以停止聚类。

剪枝条件的选择取决于聚类的目的和数据的特性。在实践中，可能需要多次尝试不同条件来找到最优的结果。

5.3.2 结果保存与Dendrogram树状图的绘制

Dendrogram（树状图）是层次聚类结果的直观表示，它通过绘制一个树状结构来展示数据点是如何被聚集成簇的。

graph TD
    A((Data Point 1))---B((Data Point 2))
    B---C((Cluster 1))
    A---D((Cluster 2))
    C---E((Cluster 3))

上图是一个简化的Dendrogram示例，展示了五个数据点如何被聚集成三个簇的过程。Dendrogram通常包含距离水平轴和簇间合并顺序的详细信息，使得用户可以轻松地理解和解释聚类过程。

聚类结果的保存也很重要。通常情况下，我们可以保存距离矩阵、聚类树、以及每个数据点所属簇的信息，这样方便后续的分析和比较。

通过本章的学习，我们已经掌握了层次聚类中的核心概念，包括距离计算方法、距离矩阵的构建、簇构建策略以及剪枝条件和结果可视化。下一章将通过对Iris数据集的分析，进一步加深理解。

本文还有配套的精品资源，点击获取

简介：层次聚类算法是一种重要的数据挖掘无监督学习方法，它通过分析数据集的内在结构来对相似数据进行分组。本项目旨在使用C++语言实现层次聚类算法，并通过分析Iris数据集来实践算法。Iris数据集包含鸢尾花的四个特征，适用于三种鸢尾花品种的分类。项目中将介绍算法的两种主要类型：凝聚型和分裂型，并详细阐述了实现的关键步骤，如距离计算、构建距离矩阵、簇的构建、剪枝条件、结果保存和可视化。通过项目实践，你将深入理解层次聚类算法的工作原理，并提升C++编程技能，特别是在数据处理和算法实现方面。

本文还有配套的精品资源，点击获取