斯皮尔皮尔森肯德尔_Pearson, Kendall, Spearman三种相关性的差异

最新推荐文章于 2024-12-17 19:56:38 发布

原创最新推荐文章于 2024-12-17 19:56:38 发布 · 3.1k 阅读

4 ·

CC 4.0 BY-SA版权

文章标签：

#斯皮尔皮尔森肯德尔

本文介绍了皮尔森、肯德尔和斯皮尔曼三种相关性分析方法，包括它们的计算公式、适用条件和解释。皮尔森相关适用于连续数据且要求数据正态分布，肯德尔秩相关是非参数检验，适用于顺序数据，斯皮尔曼等级相关同样适合顺序数据，但对分布不做假设。相关系数的强度分为极强、强、中等、弱和极弱相关。

相关性(Pearson，Kendall，Spearman)

最近在学习R语言时，需要对两个连续变量进行相关性分析，通过查看帮助文档，发现cor.test()常用的相关性方法有三种，其中出现最为频繁的就是皮尔逊相关系数了，这里收集整理一下这三种方法的区别。1

4cor.test(x, y,

alternative = c("two.sided", "less", "greater"),

method = c("pearson", "kendall", "spearman"),

exact = NULL, conf.level = 0.95, continuity = FALSE, ...)

相关性是一种双变量分析，它衡量两个变量之间关联的强度和关系的方向。关于关系的强度，相关系数的值在+1和-1之间变化。当相关系数的值在±1左右时，这被认为是两个变量之间的完美关联度。由于相关系数值为0，两个变量之间的关系将较弱。关系的方向只是+(表示变量之间的正相关)或 - (表示变量之间的负相关)相关性的符号。通常在统计学中，我们使用三种类型的相关性：Pearson相关性，Kendall秩相关性，Spearman相关.

Pearson r correlation 皮尔逊相关

Pearson r相关性是用于测量线性相关变量之间关系程度的最广泛使用的相关统计量。例如，在股票市场，如果我们想衡量两个股票之间的相互关系，则用Pearson r相关度来衡量两者之间的关系。Point-biserial相关性是用Pearson相关公式进行的，除了其中一个变量是二分的。以下公式用于计算Pearson r相关：

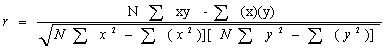
r = Pearson r相关系数

N =每个数据集中的值数

Σxy=成对分数的

乘积之和Σx= x分数

之和Σy= y分数

Σx2=平方x分数的和

Σy2=平方y得分的和

Pearson相关性可以检查的研究问题的类型：

年龄之间有统计学意义上的关系，以年数衡量，高度以英寸衡量？

温度，度数华氏度和冰淇淋销售之间是否有收入关系？

工作满意度之间是否存在关系，由JSS衡量，收入以美元衡量？

假设

对于Pearson r相关性，两个变量都应该是正态分布的(正态分布变量具有钟形曲线)。其他假设包括线性和同态性。线性度假设分析中每个变量之间存在直线关系，同质性假定数据在回归线上正态分布。

行为和解释皮尔逊相关

关键术语效应大小： Cohen的标准将用于评估相关系数，以确定关系的强度或效应大小，其中.10和.29之间的相关系数表示小关联.30和.49之间的系数表示介质关联，以及.50以上的系数表示大的关联或关系。

连续数据：间隔或比率级别的数据。这种类型的数据具有相邻单元之间的幅度和相等间隔的属性。相邻单元之间的相等间隔意味着在刻度尺上的相邻单元之间有相等量的被测量的变量。一个例子就是年龄。年龄从21岁增加到22岁将与60岁至61岁的年龄相同。

Kendall rank correlation 肯德尔等级相关

肯德尔等级相关是一个非参数检验，用于衡量两个变量之间依赖的强度。如果我们考虑两个样本a和b，其中每个样本大小为 n，我们知道与ab的配对总数为 n( n -1)/ 2。以下公式用于计算肯德尔秩相关值：

Nc =一致

Nd的数量=不一致的数量

行为和解释肯德尔相关

关键术语一致：以相同的方式订购。

不一致：有所不同。

Spearman rank correlation 斯皮尔曼等级相关

斯派曼秩相关是一个非参数测试，用于测量两个变量之间的关联程度。它是由斯皮尔曼开发的，因此称之为斯皮尔曼等级相关。斯皮尔曼等级相关性测试对于数据分布不承担任何假设，而是在以至少为次序的尺度上测量变量时进行适当的相关分析。

以下公式用于计算Spearman秩相关：

P = Spearman秩相关

di =相应值Xi和Yi的行之间的差

n n =每个数据集中的值的数量

Spearman相关答案

参与者对两个Likert量表问题的回答之间是否存在统计学上的显着关系？

马匹在种族和马的年龄之间的排名有统计学意义上的关系吗？

假设

Spearman等级相关性测试对于分布没有做任何假设。Spearman rho相关的假设是数据必须至少是序数，一个变量上的分数必须与其他变量单调相关。

行为和解释Spearman相关

关键术语效应大小： Cohen的标准将用于评估相关系数，以确定关系的强度或效应大小，其中系数在.10和.29之间表示小关联; 系数介于30.30和.49之间。并且.50及以上的系数表示大的关联或关系。

有序数据：有序量表对待测量的项目进行排序，以指示它们是否具有更多，更少或相同量的被测量变量。序数量表使我们能够确定X> Y，Y> X，或者如果X = Y。一个例子是排序舞蹈比赛的参与者。排名第一的舞者是比排名第二的舞者更好的舞者。排名第二的舞者是比排名第三的舞者更好的舞者，等等。虽然这个规模使我们能够确定大于，小于或等于，但它仍然没有定义单位之间关系的大小。