matlab cg steihaug,信赖域（一）：Cauchy Point与Dogleg

信赖域(一)：Cauchy Point与Dogleg

王金戈

从本文开始介绍优化方法的另一大类——信赖域方法。

基本思想

先回顾一下前面几篇文章介绍过的线搜索方法。在线搜索方法的每次迭代中，先确定一个搜索方向，然后沿着该方向寻找一个最佳的步长，使得目标函数在该步长下降得最多。如此迭代下去，直到满足收敛所需的条件。在确定搜索方向时，一般选择梯度下降方向或牛顿方向(即二阶近似的极小值方向)。搜索步长时，一般采用回溯法或back-and-forth方法。

信赖域方法的思路有所不同。在信赖域方法的每次迭代中，先确定一个信赖域半径，然后在该半径内计算目标函数的二阶近似的极小值。如果该极小值使得目标函数取得了充分的下降，则进入下一个迭代，并扩大信赖域半径，如果该极小值不能令目标函数取得充分的下降，则说明当前信赖域区域内的二阶近似不够可靠，需要缩小信赖域半径，重新计算极小值。如此迭代下去，直到满足收敛所需的条件。我们结合下图做进一步的解释。

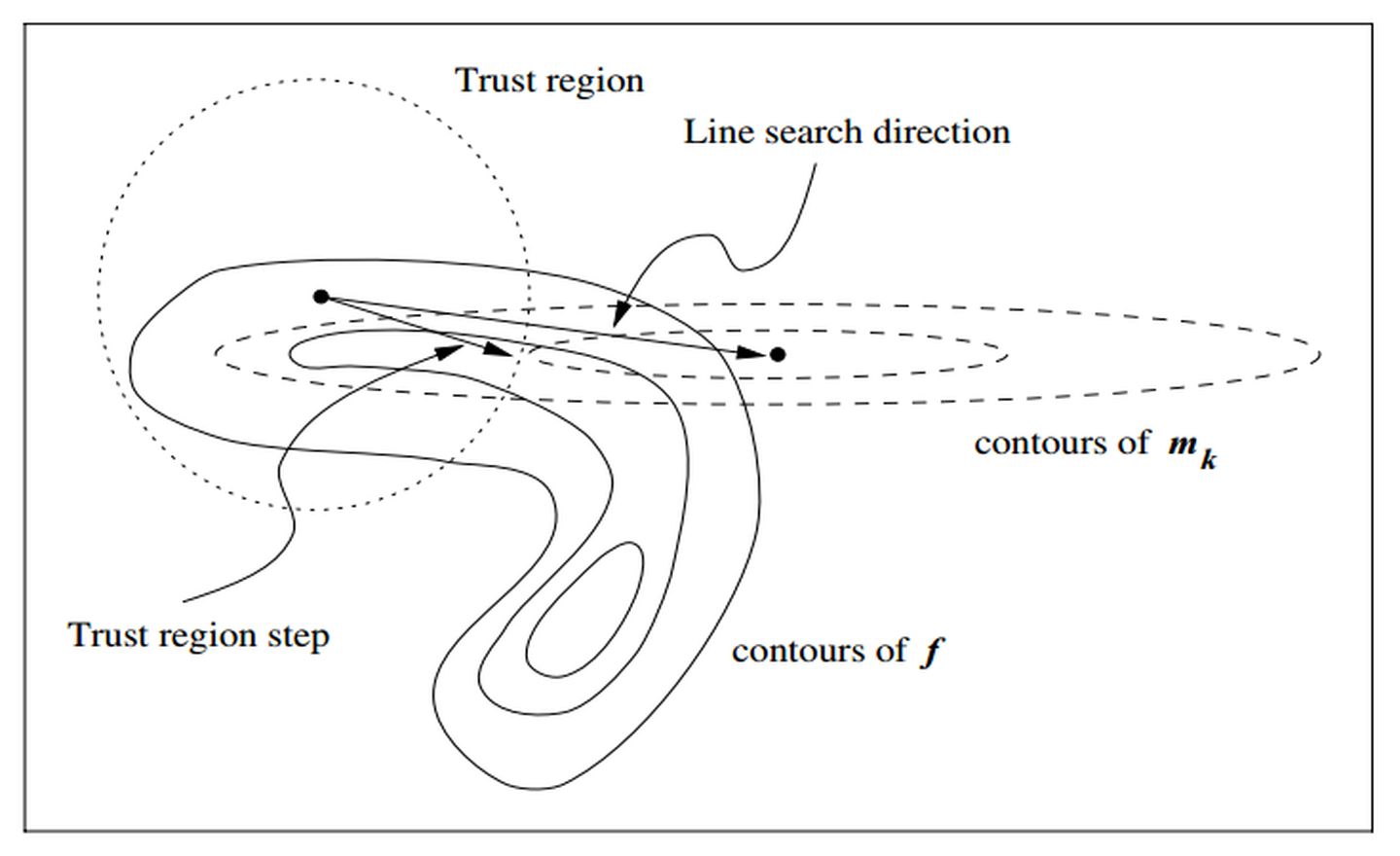
图中，实线表示了目标函数

 的等高线，它非常扭曲，因为这样更容易说明信赖域存在的价值。左上的黑点是当前位置，记作 

 ，即第 

 次迭代的初始位置。以 

 为圆心，根据信赖域半径 

 作圆，得到左上方圆形的信赖域。在 

 处对目标函数进行二阶近似，得到近似后的二阶函数

其中，

 是 

 处的海森矩阵或近似海森矩阵。在近似后的目标函数中，我们把迭代的步长(含方向) 

 作为变量，探究当 

 在信赖域范围内取何值时能够使得 

 最小。

在二维的情况下，

 的等高线是图中椭圆形的虚线。可以看到，在 

 附近，