利用指针找最大值_双指针完全攻略

Two-Pointer

双指针 two pointer 问题非常的非常的常见。一般来说，two pointer 的问题可以分为两类。

异构指针

一般是针对 array 类型的题目。array 当中有两类元素，他们 之间 或者 各自 有某种顺序。我们维护两个 pointer，每个 pointer 负责一种一类，这样就能在保证顺序的情况下，进行某种操作。

关键词：

1. array 类型
2. 两类元素
3. 有一定的有序性

可能直接这么概括比较抽象，我们来看几道 LeetCode 的高频题目。

283. Move Zeroes

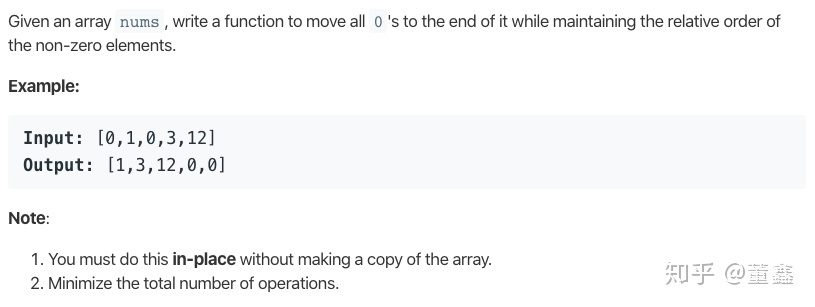
这道题的题意就是，如果你只能用交换操作，如何才能把 0 都移动到后面，并保持非零元素相对顺序不变。很明显，这道题完全符合上面总结的三种关键词。

所以这道题的思路就是，用两个 pointer ，一个 pointer 指向 当前最靠前的 0，另外遍历非零元素即可。但需要保证指向 0 的 pointer 一定要在另外一个 pointer 之前才可以。

class Solution:
    def moveZeroes(self, nums: List[int]) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        i, j = 0, 0   # i 是指向 0 的 pointer，j 是指向非零的 pointer

        while i < len(nums) and j<len(nums):
            while nums[i]!=0:
                i += 1
                if i >= len(nums):
                    return nums
                j=i

            while nums[j]==0:
                j += 1
                if j >= len(nums):
                    return nums
            nums[i], nums[j] = nums[j], nums[i]
        return nums

当然这一题还有一种比较讨巧的写法： 第一次遇到非零元素，将非零元素与数组 nums[0] 互换，第二次遇到非零元素，将非零元素与 nums[1] 互换，第三次遇到非零元素，将非零元素与 nums[2]，以此类推，直到遍历完数组

class Solution:
    def moveZeroes(self, nums: List[int]) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        i = j = 0
        for i in range(len(nums)):
            if nums[i] != 0:
                nums[j] , nums[i]= nums[i] , nums[j]
                j += 1

这种写法为什么会 work 呢？因为这么做可以保证，在进行第 n 次替换的时候，之前的非零元素已经全部完成了替换，并且全部汇集到了前 n - 1 个位置，所以本次替换一定是没有问题的。

这个其实就是后面会讲到的 Cyclic Sort 。

88. Merge Sorted Array

这个题很明显也符合上面三个关键词。但是当你去使用 two pointer 的时候，in-place 的操作会导致一些数被覆盖掉。要解决这个覆盖的问题，cost 也比较大，就是要频繁的移动 nums1。

这个时候，一个非常常用的编程思维是：

换个方向，别有洞天。

对于这道题，如果从后向前的使用 two pointer，就没有了覆盖的问题。因为后面的值本来就是没有用的，随便覆盖。

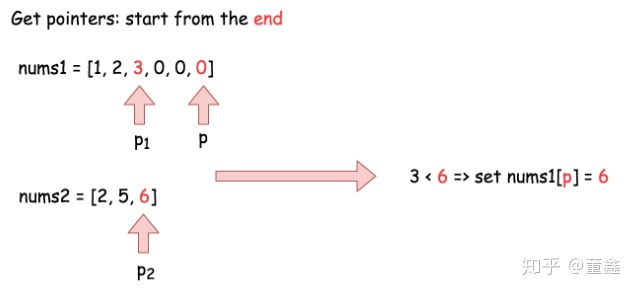
剩下的操作就跟 merge two sorted list 没什么差别了。

class Solution(object):
    def merge(self, nums1, m, nums2, n):
        """
        :type nums1: List[int]
        :type m: int
        :type nums2: List[int]
        :type n: int
        :rtype: void Do not return anything, modify nums1 in-place instead.
        """
        # two get pointers for nums1 and nums2
        p1 = m - 1
        p2 = n - 1
        # set pointer for nums1
        p = m + n - 1

        # while there are still elements to compare
        while p1 >= 0 and p2 >= 0:
            if nums1[p1] < nums2[p2]:
                nums1[p] = nums2[p2]
                p2 -= 1
            else:
                nums1[p] =  nums1[p1]
                p1 -= 1
            p -= 1

        # add missing elements from nums2
        nums1[:p2 + 1] = nums2[:p2 + 1]

FaceBook 面试真题：Dot Product of Sparse Vectors

Suppose we have very large sparse vectors (most of the elements in vector are zeros)Find a data structure to store themCompute the Dot Product. Follow-up: What if one of the vectors is very small?

很容易想到，sparse vector 可以用 dict （hashmap）来存。 对于稀疏矩阵，我们需要找到对应位置的数来乘，这个地方可以用到 two pointer 的来找。因为两个 sparse vector 的 (position, value) 可以是有序的。

a = [(1,2),(2,3),(100,5)]
b = [(0,5),(1,1),(100,6)]

i = 0; j = 0  # 两个 pointer
result = 0
while i < len(a) and j < len(b):
    if a[i][0] == b[j][0]:
        result += a[i][1] * b[j][1]
        i += 1
        j += 1
    elif a[i][0] < b[j][0]:
        i += 1
    else:
        j += 1
print(result)

二分法

二分查找也是一种非常有用的编程思想，他的实现方式也是通过不断变化左右指针得到的。

def binarySearch(nums, target):
    left, right = 0, len(nums) - 1
    while left <= right:
        mid = (right + left)/2
        if nums[mid] == target:
            return mid
        elif nums[mid] < target:
            left = mid + 1
        elif nums[mid] > target:
            right = mid - 1
    return -1

LeetCode 42. Trapping Rain Water

在解决这道题是，其实有两个难点。首先第一个难点就是，如何对这个问题建模。我们在建模的时候，不一定要顺着直观的感觉去走。比如本题中，如果直观的去建模的话，那就是要先找到有多少个“坑”，然后分别算每个“坑”能装多少水。但是当你去找“坑”的时候，你就会发现，“坑”的情况是很复杂的，而这种复杂恰恰就是程序难写的根源。

对于这一题，有一个非常简单的方法可以解决。我们现在不去找有多少坑，而是看每一个 bin 能对最终装水贡献多少。

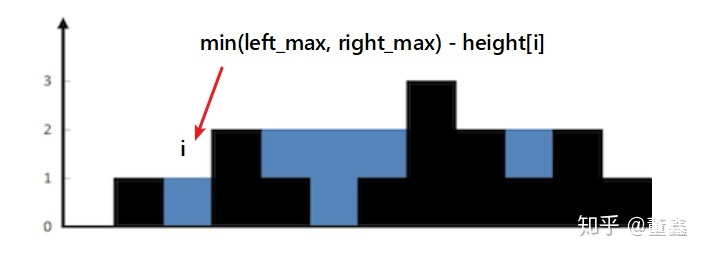
比如上面图中的第一个bin，贡献是 0，第二个贡献也是 0，而第三个贡献是 1.第四个贡献是 0，第五个贡献是 1，第六个贡献是 2...

实际上：

位置 i 能容下雨水量:

所以，问题就变成了：如何找所有位置的左右两边的柱子的最大值？

很明显，我们可以用三种方法来解决：

1. 动态规划

我们可以分别算每个位置的左边最大值和右边最大值。

class Solution:
    def trap(self, height: List[int]) -> int:
        if not height: return 0
        n = len(height)
        max_left = [0] * n
        max_right = [0] * n
        max_left[0] = height[0]
        max_right[-1] = height[-1]
        # 找位置i左边最大值
        for i in range(1, n):
            max_left[i] = max(height[i], max_left[i-1])
        # 找位置i右边最大值
        for i in range(n-2, -1, -1):
            max_right[i] = max(height[i], max_right[i+1])
        #print(max_left)
        #print(max_right)
        # 求结果
        res = 0
        for i in range(n):
            res += min(max_left[i], max_right[i]) - height[i]
        return res

2. 栈

这道题，直观上讲，如果想找能盛水的柱子，肯定要有回退操作的。因为只有确定了后面有更高的柱子，才能确定某个柱子能装水。凡是有这种需要回退的题目，栈都是一个非常好的选择。

如果要用栈的，基本思路是，如果待入栈元素比栈顶小，直接入栈。反之，栈顶元素出栈，进行计算，然后再入栈。这样的一个栈，很明显就是一个单调栈。

class Solution:
    def trap(self, height: List[int]) -> int:
        if not height: return 0
        n = len(height)
        stack = []
        res = 0
        for i in range(n):
            #print(stack)
            while stack and height[stack[-1]] < height[i]:
                tmp = stack.pop()
                if not stack: break
                res += (min(height[i], height[stack[-1]]) - height[tmp]) * (i-stack[-1] - 1)
            stack.append(i)
        return res

3. 双指针

这一题用双指针来写还是有些难度的，思路会比较绕，这里详细的说一说。用双指针解，和上面解法相比的好处在于空间复杂度是 O(1)，也就是常说的边走边算，不用额外存储一些东西。

首先我们定义两个指针，left 和 right，前者从最左边开始，后者从最右边开始。然后我们维护两个最大值,l_max是height[0..left]中最高柱子的高度，r_max是height[right..end]的最高柱子的高度。

上面提到过，每个柱子能装的水的量是由

决定的。

但是仔细分析会发现，我们要得到这个值并不一定非得把

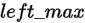
和

都算出来。例如，如果我们知道l_max < r_max，至于这个 r_max 是不是右边最大的，无所谓。现有的信息足够我们算出

一定是l_max。

class Solution:
    def trap(self, height: List[int]) -> int:
        if not height: return 0
        left = 0
        right = len(height) - 1
        res = 0
        # 记录左右边最大值
        left_max = height[left]
        right_max = height[right]
        while left < right:
            if left_max < right_max:
                res += left_max - height[left]
                left += 1
                left_max = max(left_max, height[left])
            else:
                res += right_max - height[right]
                right -= 1
                right_max = max(right_max, height[right])
        return res

这道题还是比较难的，下面总结一下这道题目。

对暴力解法的思考是很重要的，暴力解法是优化解法的基础。通过对暴力解法的思考、分析，可以帮助我们得到一些优化解法的细节和思路。这道题难就难在，暴力枚举的方法都不是很好看出来。 所以对于这种问题，我们不要想整体，而应该去想局部。对于这道题，我们不要去想每个坑的情况，而应该去想每个柱子的情况。

快慢指针

快慢指针一般用于链表。为什么链表的问题，很多都要用到快慢指针呢？因为链表的 idexing 是很弱的，每次只能看到自己的 next（非常“短视”）。通过快慢指针，我们可以“之后”或者“之前”的一些元素，实际上是增加了“视野”。

下面看几道题目。

判断链表是否有环

经典解法就是用两个指针，一个每次前进两步，一个每次前进一步。如果不含有环，跑得快的那个指针最终会遇到 null，说明链表不含环；如果含有环，快指针最终会超慢指针一圈（只要有环，总是能追的上），和慢指针相遇，说明链表含有环。

def hasCyle(head):
        fast, slow = head, head

        while (fast != None) and (fast.next != None):
            fast = fast.next.next
            slow = slow.next
            if fast == slow:
                return True

        return False

已知链表有环，找到环的起点

当快慢指针相遇时，让其中任一个指针重新指向头节点，然后让它俩以相同速度前进，再次相遇时所在的节点位置就是环开始的位置。这里就不展开分析了。

类似的思路，还可以解决“寻找链表中点”的问题。还是让快指针每次走两步，慢指针走一步，当快指针走到尽头，慢指针就正好在中点位置上。还有“寻找链表的倒数第 k 个元素，让快指针先走 k 步，然后快慢指针开始同速前进。这样当快指针走到链表末尾 null 时，慢指针所在的位置就是倒数第 k 个链表节点。