数学定义[编辑]
若k个随机变量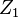 、……、
、……、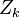 是相互独立,符合标准正态分布的随机变量(数学期望为0、方差为1),则随机变量Z的平方和
是相互独立,符合标准正态分布的随机变量(数学期望为0、方差为1),则随机变量Z的平方和
被称为服从自由度为 k 的卡方分布,记作
-
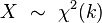
-
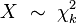
-
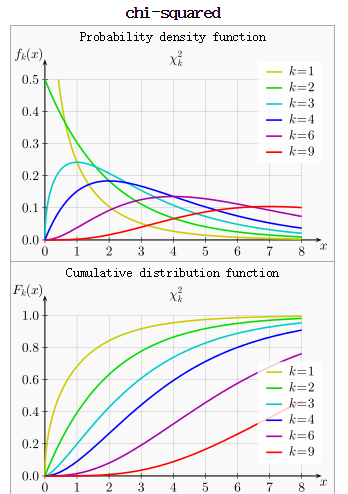
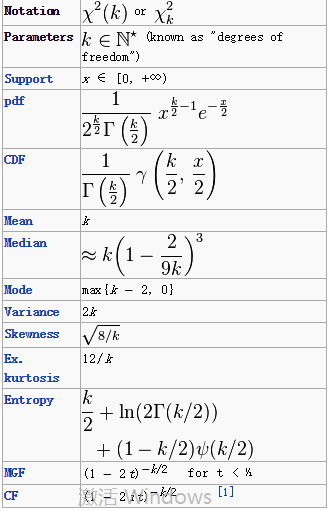
Definition[edit]
If Z1, ..., Zk are independent, standard normal random variables, then the sum of their squares,
is distributed according to the chi-squared distribution with k degrees of freedom. This is usually denoted as
The chi-squared distribution has one parameter: k — a positive integer that specifies the number of degrees of freedom (i.e. the number of Zi’s)
(应用原理没搞懂)
-




 本文介绍了卡方分布的基本概念及其数学定义。当多个独立的标准正态分布随机变量的平方和形成新的随机变量时,该变量服从特定的卡方分布。文中还提到了卡方分布的一个参数——自由度k,它决定了分布的形态。
本文介绍了卡方分布的基本概念及其数学定义。当多个独立的标准正态分布随机变量的平方和形成新的随机变量时,该变量服从特定的卡方分布。文中还提到了卡方分布的一个参数——自由度k,它决定了分布的形态。
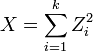
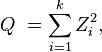
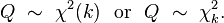
















 262
262

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








