clc; clear; close all; ld=400; %定义学习样本的数量 x=rand(2,ld); %得到一个2 * 400的一个矩阵,每个元素在0-1之间 x=(x-0.5)*1.5*2; %-1.5, 1.5 x1=x(1,:); %得到矩阵的第1行 x2=x(2,:); %得到矩阵的第2行 F=20+x1.^2-10*cos(2*pi*x1)+x2.^2-10*cos(2*pi*x2); %定义样本输出 %训练网络 net=newrb(x,F); %generate the testing data interval=0.1; [i, j]=meshgrid(-1.5:interval:1.5); row=size(i); tx1=i(:); %列矩阵 tx1=tx1'; %变为行矩阵 tx2=j(:); tx2=tx2'; tx=[tx1;tx2]; %2 * n的矩阵 ,作为测试网络的输入数据 %testing ty=sim(net,tx); %调用网络,得到对应的输出结果 % 画出网络得到的结果 v=reshape(ty,row); figure subplot(1,3,2) mesh(i,j,v); zlim([0,60]) %plot the original function interval=0.1; [x1, x2]=meshgrid(-1.5:interval:1.5); F = 20+x1.^2-10*cos(2*pi*x1)+x2.^2-10*cos(2*pi*x2); subplot(1,3,1) mesh(x1,x2,F); zlim([0,60]) %plot the error subplot(1,3,3) mesh(x1,x2,F-v); zlim([0,60])
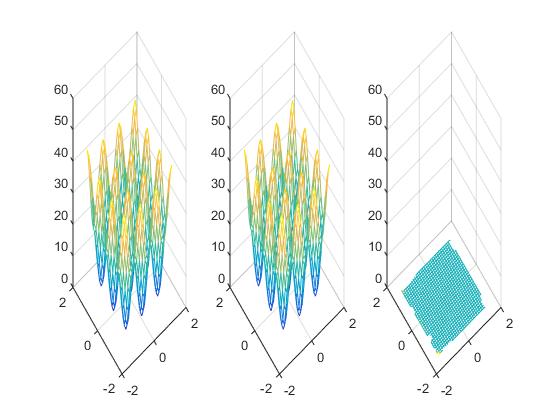




 本文通过MATLAB代码演示了如何使用径向基函数(RBF)网络进行函数逼近。首先生成了训练样本,并利用这些样本训练了一个RBF网络。接着生成了测试数据并对网络进行了测试。最后将网络预测结果与原始函数进行了对比,并展示了误差分布。
本文通过MATLAB代码演示了如何使用径向基函数(RBF)网络进行函数逼近。首先生成了训练样本,并利用这些样本训练了一个RBF网络。接着生成了测试数据并对网络进行了测试。最后将网络预测结果与原始函数进行了对比,并展示了误差分布。
















 1231
1231

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








