NOIP 提高组 2014 飞扬的小鸟(记录结果再利用的DP)

最新推荐文章于 2025-09-07 20:32:33 发布

weixin_30929011

最新推荐文章于 2025-09-07 20:32:33 发布

阅读量87

点赞数

CC 4.0 BY-SA版权

文章标签：数据结构与算法

原文链接：http://www.cnblogs.com/violet-acmer/p/9943103.html

传送门

https://www.cnblogs.com/violet-acmer/p/9937201.html

参考资料：

　　[1]:https://www.luogu.org/blog/xxzh2425/fei-yang-di-xiao-niao-ti-xie-p1941-post

　　[2]:https://www.luogu.org/blog/JOE/solution-p1941

需注意的地方：

　　(1):在每一时刻都可以点击屏幕好多好多次，就算是在m高度处也可以点击屏幕使其保持在最高点。

题解：

　　相关变量解释：

 1 int n,m,k;
 2 int x[maxn];//x[i] : 在X=i处点击屏幕，在i+1处上升x[i]高度
 3 int y[maxn];//y[i] : 在X=i处不点击屏幕，在i+1处下降y[i]高度
 4 struct Node
 5 {
 6     int id;//水管的编号
 7     int l,h;//l : 下边界； h : 下边界
 8     Node(int a=0,int b=0,int c=0):id(a),l(b),h(c){}
 9 }pipeline[maxn];//水管信息
10 int dp[maxn][2*1000];//dp[i][j] : 来到i处的j高度所需的最少的点击量，至于为什么列要开2*1000，一会解释

　　根据dp定义，很容易写出状态转移方程：

1 dp[i][j]=min(dp[i][j],dp[i-1][j-k*x[i-1]]+k);
2 dp[i][j]=min(dp[i][j],dp[i-1][j+y[i-1]]);

　　1是指从(i-1,j-k*x[i-1])处点击屏幕k次来到(i,j)处

　　2是指从(i-1,j+y[i-1])处不点击屏幕来到(i,j)处，最终答案就是1,2中最小的那个

　　如果将此状态写出的代码提交上去，会超时的，为什么呢？

　　因为每个点(i,j)都需要循环 k 次来找出最小点击量，这就是O(Σⁿ_i=1Σ^m_j=1kj)的复杂度，而O(Σⁿ_i=1Σ^m_j=1kj)最大为O(n*m²)。

　　那要怎么办呢？注意观察一下：

　　假设来到(i,10)处，x[i-1]=3

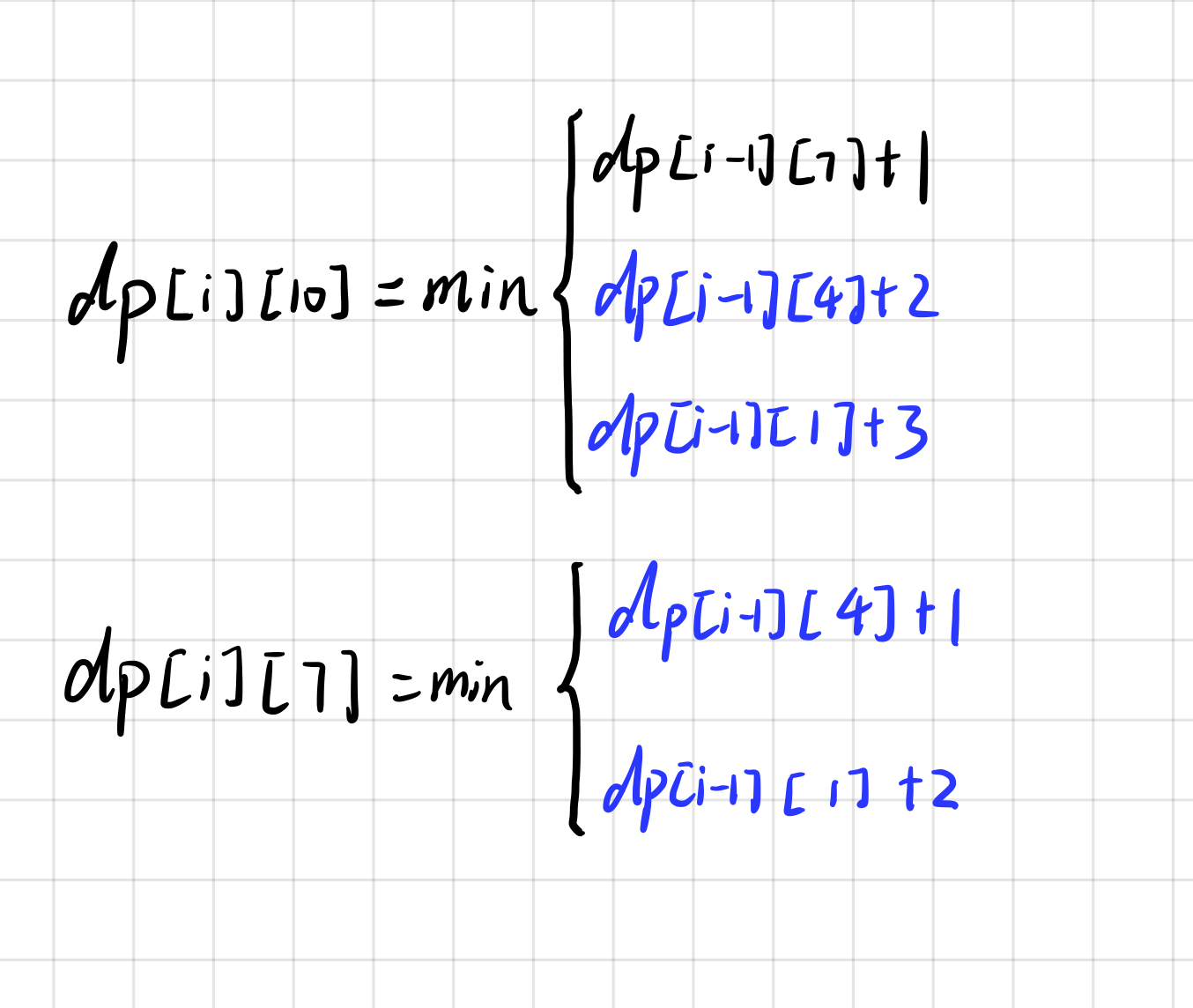
　　在计算dp[ i ][10]的时候，dp[ i-1][4],dp[ i-1][1]相对大小已经在计算dp[i][7]的时候计算过了，所以应利用好之前的结果，那么状态转移方程就变为：

1 dp[i][j]=min(dp[i-1][j-x[i-1]]+1,dp[i][j-x[i-1]]+1);
2 dp[i][j]=min(dp[i][j],dp[i-1][j+y[i-1]]);

　　下面来证明一下正确性：

　　如果dp[i][7]=dp[i-1][4] => dp[i-1][4]+1 < dp[i-1][1]+2;

　　方程两端同时加上1 => dp[i-1][4]+2 < dp[i-1][1]+3,那来到 j = 10时，dp[i-1][4]+2与dp[i-1][1]+3的相对大小已经在求解dp[i][7]的时候求解出来了。

　　根据上述转移方程得到：

 1 void updataDp(int i,int a,int b)
 2 {
 3     for(int j=1+x[i-1];j <= m+x[i-1];++j)//从(i-1,j-x[i-1])处点击屏幕来到(i,j)处
 4         dp[i][j]=min(dp[i-1][j-x[i-1]]+1,dp[i][j-x[i-1]]+1);
 5     
 6     for(int j=1;j < m;++j)//特判(i,m)点
 7     {
 8         int tot=(m-j)/x[i-1];
 9         while(j+tot*x[i-1] < m)
10             tot++;
11         dp[i][m]=min(dp[i][m],dp[i-1][j]+tot);
12     }
13     
14     for(int j=1;j+y[i-1] <= m;++j)//从(i-1,j+y[i-1])处不点击屏幕来到(i,j)处
15         dp[i][j]=min(dp[i][j],dp[i-1][j+y[i-1]]);
16   
17     dp[i][m]=min(dp[i][m],dp[i-1][m]+1);//就算在i-1处到达m点，也可以通过点击一次屏幕来到(i,m)处
18 
19     for(int j=1;j < a;++j)//[a,b]是i处无管道的区域，[a,b]之外都不可达，所以赋值为INF
20         dp[i][j]=INF;
21     for(int j=b+1;j <= m;++j)
22         dp[i][j]=INF;
23 }

　　其中(i,m)点的特判可改为

1 for(int j=m+1;j <= m+x[i-1];++j)
2     dp[i][m]=min(dp[i][m],dp[i][j]);

　　这是为什么第一个for( )的范围最大到 m+x[i-1]，以及dp[][]的列开到2*1000的原因；

AC代码：

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<algorithm>
 5 using namespace std;
 6 #define INF 0x3f3f3f3f
 7 #define mem(a,b) memset(a,b,sizeof(a))
 8 const int maxn=1e4+50;
 9 
10 int n,m,k;
11 int x[maxn];//x[i] : 在X=i处点击屏幕，在i+1处上升x[i]高度
12 int y[maxn];//y[i] : 在X=i处不点击屏幕，在i+1处下降y[i]高度
13 struct Node
14 {
15     int id;//水管的编号
16     int l,h;//l : 下边界； h : 下边界
17     Node(int a=0,int b=0,int c=0):id(a),l(b),h(c){}
18 }pipeline[maxn];//水管信息
19 int dp[maxn][2*1000];//dp[i][j] : 来到i处的j高度所需的最少的点击量，至于为什么列要开2*1000，一会解释
20 bool cmp(Node _a,Node _b){
21     return _a.id < _b.id;//按照管道编号升序排列
22 }
23 void Updata(int &a,int &b,int &ki,int i)//更新 X=i 处的上下边界
24 {
25     if(ki <= k && pipeline[ki].id == i)
26         a=pipeline[ki].l+1,b=pipeline[ki].h-1,ki++;
27 }
28 void updataDp(int i,int a,int b)
29 {
30     for(int j=1+x[i-1];j <= m+x[i-1];++j)//从(i-1,j-x[i-1])处点击屏幕来到(i,j)处
31         dp[i][j]=min(dp[i-1][j-x[i-1]]+1,dp[i][j-x[i-1]]+1);
32 
33     for(int j=1;j < m;++j)//特判(i,m)点
34     {
35         int tot=(m-j)/x[i-1];
36         while(j+tot*x[i-1] < m)
37             tot++;
38         dp[i][m]=min(dp[i][m],dp[i-1][j]+tot);
39     }
40 
41     for(int j=1;j+y[i-1] <= m;++j)//从(i-1,j+y[i-1])处不点击屏幕来到(i,j)处
42         dp[i][j]=min(dp[i][j],dp[i-1][j+y[i-1]]);
43 
44     dp[i][m]=min(dp[i][m],dp[i-1][m]+1);//就算在i-1处到达m点，也可以通过点击一次屏幕来到(i,m)处
45 
46     for(int j=1;j < a;++j)//[a,b]是i处无管道的区域，[a,b]之外都不可达，所以赋值为INF
47         dp[i][j]=INF;
48     for(int j=b+1;j <= m;++j)
49         dp[i][j]=INF;
50 }
51 int Check()
52 {
53     int res=dp[0][0];
54     for(int i=1;i <= m;++i)
55         res=min(dp[n][i],res);
56     return res;
57 }
58 int maxPass()
59 {
60     for(int ki=k;ki >= 1;--ki)
61         for(int i=pipeline[ki].l+1;i < pipeline[ki].h;++i)
62             if(dp[pipeline[ki].id][i] < INF)//为什么用 < 而不是用 != 呢？
63                 return ki;
64     return 0;
65 }
66 void Solve()
67 {
68     sort(pipeline+1,pipeline+k+1,cmp);
69     mem(dp,INF);
70     for(int i=1;i <= m;++i)
71         dp[0][i]=0;
72     int ki=1;
73     for(int i=1;i <= n;++i)
74     {
75         int a=1,b=m;
76         Updata(a,b,ki,i);//更新i处的无管道范围[a,b]
77         updataDp(i,a,b);
78     }
79     int res=Check();
80     if(res < INF)//为什么用 < 而不是用 != 呢？
81         printf("%d\n%d\n",1,res);
82     else
83         printf("%d\n%d\n",0,maxPass());
84 }
85 int main()
86 {
87     scanf("%d%d%d",&n,&m,&k);
88     for(int i=0;i < n;++i)
89         scanf("%d%d",x+i,y+i);
90     for(int i=1;i <= k;++i)
91     {
92         int a,b,c;
93         scanf("%d%d%d",&a,&b,&c);
94         pipeline[i]=Node(a,b,c);
95     }
96     Solve();
97 }

View Code

　　对代码中的问题解释一下，这是我下午踩的一个坑：

　　看updataDp中的第一个for()

1 for(int j=1+x[i-1];j <= m+x[i-1];++j)
2     dp[i][j]=min(dp[i-1][j-x[i-1]]+1,dp[i][j-x[i-1]]+1);

　　如果dp[i-1][j-x[i-1]] == INF 且 dp[i][j-x[i-1]] == INF，那dp[ i ][ j ] == INF+1 > INF;。

　　还发现一个有趣的地方：

　　mem(dp,0x3f) <=> mem(dp,0x3f3f3f3f)

　　但是 0x3f < 0x3f3f3f3f

转载于:https://www.cnblogs.com/violet-acmer/p/9943103.html