[BZOJ1721][Usaco2006 Mar]Ski Lift 缆车支柱

转载于 2019-03-07 19:22:00 发布 · 79 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/zhenglw/p/10491720.html

本文通过数学分析和动态规划(DP)方法，解决了一个斜率优化问题，详细介绍了如何通过判断两点间的连线斜率来优化解决方案，最终实现O(N^2)的时间复杂度。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

日常吐槽：最大值赋太大79分卡了好久好久

算法：DP

分析：数学分析一下即可

最优解肯定是介个样子的：

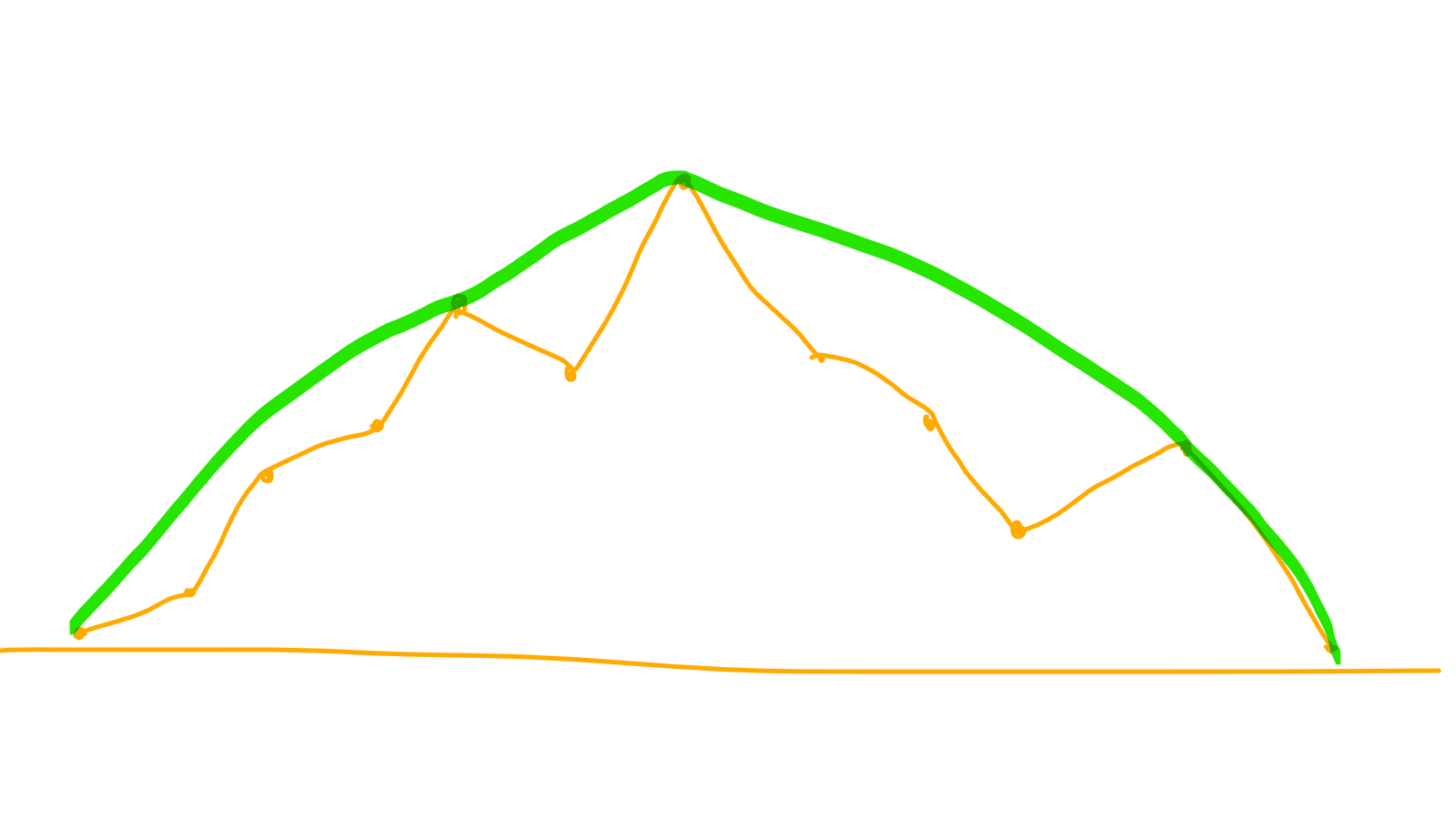
抽象一点的话：

也就是说两个点（i,j）之间如果能够连上线，则必定中间点对（i,k(k∈(i,j))）没有斜率比它（i,j）大的

然后DP暴力更新，O(NM)---->O(N^2)

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<algorithm>
 5 #define int long long
 6 using namespace std;
 7 inline int read(){
 8     char chr=getchar();    int f=1,ans=0;
 9     while(!isdigit(chr)) {if(chr=='-') f=-1;chr=getchar();}
10     while(isdigit(chr))  {ans=(ans<<3)+(ans<<1);ans+=chr-'0';chr=getchar();}
11     return ans*f;
12 }int n,m,h[5005],dp[5005];long double k,maxn;
13 signed main(){
14     n=read(),m=read();for(int i=1;i<=n;i++)h[i]=read();
15     for(int i=1;i<=n;i++)dp[i]=9223372036854775803ll;dp[1]=1;
16     for(int i=1;i<=n;i++){
17         maxn=-2147483647;
18         for(int j=1;i+j<=n&&j<=m;j++)
19             k=(h[i+j]-h[i])*1.0/(j*1.0),(k>=maxn)?(dp[i+j]=min(dp[i+j],dp[i]+1),maxn=k):1;
20     }cout<<dp[n];
21     return 0;
22 }