poj 2411 Mondriaan's Dream（状态压缩dp）

最新推荐文章于 2021-03-30 20:02:40 发布

转载最新推荐文章于 2021-03-30 20:02:40 发布 · 45 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/UniqueColor/p/4810487.html

本文介绍了一种使用动态规划算法解决矩形填充问题的方法。该问题要求计算不同方式用1x2矩形块完全覆盖一个较大矩形的数量。通过定义状态和转移方程，文章详细解释了如何高效地求解这一问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

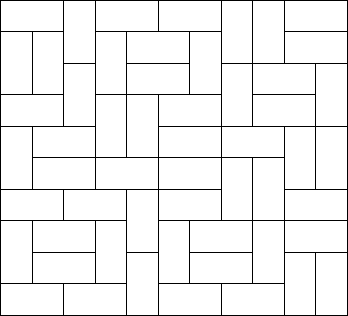
Description

Squares and rectangles fascinated the famous Dutch painter Piet Mondriaan. One night, after producing the drawings in his 'toilet series' (where he had to use his toilet paper to draw on, for all of his paper was filled with squares and rectangles), he dreamt of filling a large rectangle with small rectangles of width 2 and height 1 in varying ways.

Expert as he was in this material, he saw at a glance that he'll need a computer to calculate the number of ways to fill the large rectangle whose dimensions were integer values, as well. Help him, so that his dream won't turn into a nightmare!

Input

The input contains several test cases. Each test case is made up of two integer numbers: the height h and the width w of the large rectangle. Input is terminated by h=w=0. Otherwise, 1<=h,w<=11.

Output

For each test case, output the number of different ways the given rectangle can be filled with small rectangles of size 2 times 1. Assume the given large rectangle is oriented, i.e. count symmetrical tilings multiple times.

Sample Input

Sample Output

Source

Ulm Local 2000

【题目大意】一个矩阵，只能放1*2的木块，问将这个矩阵完全覆盖的不同放法有多少种。

【解析】如果是横着的就定义11，如果竖着的定义为竖着的01，这样按行dp只需要考虑两件事儿，当前行&上一行，是不是全为1，不是说明竖着有空（不可能出现竖着的00），另一个要检查当前行里有没有横放的，但为奇数的1。

【状态表示】dp[state][i]第i行状态为state时候的方案数

【转移方程】dp[state][i] += dp[state'][i-1] state'为i-1行的，不与i行状态state冲突的状态

【边界条件】第一行符合条件的状态记为1 即dp[state][0] = 1;

 1 #pragma comment(linker, "/STACK:1024000000,1024000000")
 2 #include<iostream>
 3 #include<cstdio>
 4 #include<cstring>
 5 #include<cmath>
 6 #include<math.h>
 7 #include<algorithm>
 8 #include<queue>
 9 #include<set>
10 #include<bitset>
11 #include<map>
12 #include<vector>
13 #include<stdlib.h>
14 using namespace std;
15 #define max(a,b) (a) > (b) ? (a) : (b)  
16 #define min(a,b) (a) < (b) ? (a) : (b)
17 #define ll long long
18 #define eps 1e-10
19 #define MOD 1000000007
20 #define N 16
21 #define M 1<<16
22 #define inf 1e12
23 ll n,m;
24 ll dp[N][M];
25 ll state_true[M];
26 ll total;
27 ll nowTotal;
28 bool judge(ll s){
29     ll ans=0;
30     while(s>0){
31         if((s&1)==1){
32             ans++;
33         }
34         else{
35             if((ans&1)==1){
36                 return false;
37             }
38             ans=0;
39         }
40         s>>=1;
41     }
42     if((ans&1)==1)
43        return false;
44      return true;
45 }
46 void init(){
47      total=(1<<16);
48     for(ll S=0;S<total;S++){
49         if(judge(S)){
50             state_true[S]=1;
51         }
52     }
53 }
54 bool check(ll s1,ll s2){
55     if( (s1 | s2) != (nowTotal-1) ){
56         return false;
57     }
58     return state_true[s1&s2];
59 }
60 int main()
61 {
62     init();
63     while(scanf("%I64d%i64d",&n,&m)==2){
64         if(n==0 && m==0) break;
65         
66         nowTotal=(1<<m);
67         memset(dp,0,sizeof(dp));
68         for(ll S=0;S<nowTotal;S++){
69             if(state_true[S]){
70                 dp[0][S]=1;
71             }
72         }
73         for(ll i=1;i<n;i++){
74             for(ll S1=0;S1<nowTotal;S1++){
75                 for(ll S2=0;S2<nowTotal;S2++){
76                     if(check(S1,S2)){
77                         dp[i][S1]+=dp[i-1][S2];
78                     }
79                 }
80             }
81         }
82         printf("%I64d\n",dp[n-1][nowTotal-1]);
83     }
84     return 0;
85 }

View Code

转载于:https://www.cnblogs.com/UniqueColor/p/4810487.html