2018 ICPC青岛网络赛 B. Red Black Tree(倍增lca)

最新推荐文章于 2025-08-07 23:59:18 发布

转载最新推荐文章于 2025-08-07 23:59:18 发布 · 201 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/iwannabe/p/10897423.html

文章标签：

#ui

博客围绕树节点查询问题展开，给出一棵树，部分点为红色，其余为黑色，定义点的花费为到最近红色祖先节点的距离。q次查询，每次给出k个节点，允许将最多一个黑点变红，求k个点最大花费的最小值。介绍了通过二分查找求解的思路。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

BaoBao has just found a rooted tree with n vertices and (n-1) weighted edges in his backyard. Among the vertices, m of them are red, while the others are black. The root of the tree is vertex 1 and it’s a red vertex.
Let’s define the cost of a red vertex to be 0, and the cost of a black vertex to be the distance between this vertex and its nearest red ancestor.
Recall that

The length of a path on the tree is the sum of the weights of the edges in this path.
The distance between two vertices is the length of the shortest path on the tree to go from one vertex to the other.
Vertex u is the ancestor of vertex v if it lies on the shortest path between vertex v and the root of the tree (which is vertex 1 in this problem).

As BaoBao is bored, he decides to play q games with the tree. For the i-th game, BaoBao will select k_i vertices v_i,1, v_i,2, . . . , v_i,ki on the tree and try to minimize the maximum cost of these k_i vertices by changing at most one vertex on the tree to a red vertex.
Note that

BaoBao is free to change any vertex among all the n vertices to a red vertex, NOT necessary among the ki vertiecs whose maximum cost he tries to minimize.
All the q games are independent. That is to say, the tree BaoBao plays with in each game is always the initial given tree, NOT the tree modiﬁed during the last game by changing at most one vertex.

Please help BaoBao calculate the smallest possible maximum cost of the given k_i vertices in each game after changing at most one vertex to a red vertex.

输入

There are multiple test cases. The first line of the input is an integer T, indicating the number of test cases. For each test case:
The first line contains three integers n, m and q (2≤m≤n≤10⁵, 1≤q≤2×10⁵), indicating the size of the tree, the number of red vertices and the number of games.
The second line contains m integers r₁, r₂, . . . , r_m (1 = r₁ < r₂ <...< r_m≤n), indicating the red vertices.
The following (n-1) lines each contains three integers u_i, v_i and w_i (1≤u_i, v_i≤n, 1≤w_i≤10⁹),indicating an edge with weight wi connecting vertex ui and vi in the tree.
For the following q lines, the i-th line will first contain an integer k_i (1≤k_i≤n). Then k_i integers v_i,1, v_i,2, . . . , v_i,ki follow (1≤v_i,1 < v_i,2 < ... < v_i,ki≤n), indicating the vertices whose maximum cost BaoBao has to minimize.
It’s guaranteed that the sum of n in all test cases will not exceed 106, and the sum of k_i in all test cases will not exceed 2×10⁶.

输出

For each test case output q lines each containing one integer, indicating the smallest possible maximum cost of the k_i vertices given in each game after changing at most one vertex in the tree to a red vertex.

样例输入

2
12 2 4
1 9
1 2 1
2 3 4
3 4 3
3 5 2
2 6 2
6 7 1
6 8 2
2 9 5
9 10 2
9 11 3
1 12 10
3 3 7 8
4 4 5 7 8
4 7 8 10 11
3 4 5 12
3 2 3
1 2
1 2 1
1 3 1
1 1
2 1 2
3 1 2 3

样例输出

提示

The first sample test case is shown above. Let’s denote C(v) as the cost of vertex v.
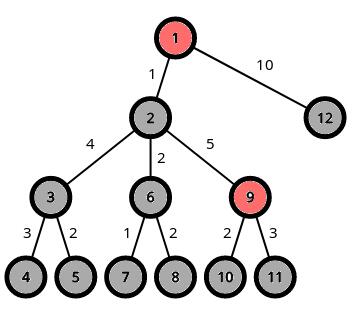
For the 1st game, the best choice is to make vertex 2 red, so that C(3) = 4, C(7) = 3 and C(8) = 4. So the answer is 4.
For the 2nd game, the best choice is to make vertex 3 red, so that C(4) = 3, C(5) = 2, C(7) = 4 and C(8) = 5. So the answer is 5.
For the 3rd game, the best choice is to make vertex 6 red, so that C(7) = 1, C(8) = 2, C(10) = 2 and C(11) = 3. So the answer is 3.
For the 4th game, the best choice is to make vertex 12 red, so that C(4) = 8, C(5) = 7 and C(12) = 0.
So the answer is 8.

题意：

给出一棵树，其中某些点是红色，其余点是黑色。定义一个点的花费为这个点到距其最近的红色祖先节点的距离。q次查询，每次查询给出k个节点，允许将最多一个黑色点变为红色，求这k个点中最大花费的最小值。每次查询相互独立，不影响树的初始结构。

思路:因为要减小指定点的花费，那么很明显，这个变成红色的节点应该在这些节点的所有最近公共祖先中

我们可以二分这些点去寻找，那么二分就应该先找出单调性，先预处理出每个点的花费和其直接到根节点的花费，顺便处理出st表求lca所需要的值

然后二分其花费值，找到最小的满足情况的值

对于二分，我们应该从大到小把节点按照其花费排序，然后检查，如果第一个点，也就是最大的点就<=二分值就可以直接退出（满足情况），否则就遍历节点，求他们的lca（说明要找到一个他们的公共祖先，变成红色，减小花费），直到其花费<=二分值mid。

然后检查之前求出的，把lca变红后，其花费min(原本花费，其到根花费-lca到根花费)是否都满足<=mid，不是就return 0；

  1 #include<bits/stdc++.h>
  2 using namespace std;
  3  
  4 const int maxn = 1e5+5;
  5 int T;
  6 int n,m,q;
  7  
  8 typedef long long ll;
  9 struct Node
 10 {
 11     int y,next;
 12     int w;
 13 } node[maxn<<1];
 14 int cnt,head[maxn];
 15 bool isRED[maxn];
 16 int subnum[maxn];
 17 void add(int x,int y,int w)
 18 {
 19     node[++cnt].y=y;
 20     node[cnt].w=w;
 21     node[cnt].next=head[x];
 22     head[x]=cnt;
 23 }
 24  
 25 ll dis[maxn];
 26 ll DIS[maxn];
 27 int R[maxn];
 28  
 29 int d[maxn<<1],tot;
 30 int first[maxn<<1];
 31 int rmq[maxn<<1];
 32  
 33 void init()
 34 {
 35     cnt=tot=0;
 36     memset(isRED,0,sizeof(isRED));
 37     memset(head,0,sizeof(head));
 38 }
 39  
 40 void dfs(int x,int f,int dep)
 41 {
 42     if(isRED[x])R[x]=x;
 43     else R[x] = R[f];
 44     first[x]=++tot;
 45     rmq[tot]=x;
 46     d[tot] = dep;
 47     DIS[x] = dis[x] - dis[R[x]];
 48     for(int i=head[x]; i; i=node[i].next)
 49     {
 50         int y=node[i].y;
 51         if(y == f)continue;
 52         dis[y]=dis[x]+node[i].w;
 53         dfs(y,x,dep+1);
 54         rmq[++tot]=x;
 55         d[tot]=dep;
 56     }
 57 }
 58  
 59 struct ST
 60 {
 61     int m[maxn<<1];
 62     int dp[maxn<<1][20];
 63     void init(int n)
 64     {
 65         m[0]=-1;
 66         for(int i=1; i<=n; i++)
 67         {
 68             m[i] = ((i&(i-1)) == 0)?m[i-1]+1:m[i-1];
 69             dp[i][0]=i;
 70         }
 71         for(int j=1; (1<<j)<=n; j++)
 72         {
 73             for(int i=1; i+(1<<j)-1<=n; i++)
 74             {
 75                 int a = dp[i][j-1];
 76                 int b = dp[i+(1<<(j-1))][j-1];
 77                 dp[i][j] = d[a] < d[b]?a:b;
 78             }
 79         }
 80     }
 81     int RMQ(int l,int r)
 82     {
 83         int k=m[r-l+1];
 84         int a = dp[l][k];
 85         int b = dp[r-(1<<k)+1][k];
 86         if(d[a] < d[b])return rmq[a];
 87         return rmq[b];
 88     }
 89  
 90 } ST;
 91 bool cmp(int a,int b)
 92 {
 93     return DIS[a] > DIS[b];
 94 }
 95 bool check(ll mid,int n)
 96 {
 97     if(DIS[subnum[1]] <= mid)return 1;
 98     int lca = subnum[1];
 99     for(int i=2; i<=n; i++)
100     {
101         if(DIS[subnum[i]] <= mid)break;
102         int a = first[lca];
103         int b = first[subnum[i]];
104         if(a > b)swap(a,b);
105         lca = ST.RMQ(a,b);
106     }
107     for(int i=1; i<=n; i++)
108     {
109         if(DIS[subnum[i]] <= mid)return 1;
110         if(dis[subnum[i]] - dis[lca] > mid)return 0;
111     }
112     return 1;
113 }
114 int main()
115 {
116     scanf("%d",&T);
117     while(T--)
118     {
119         scanf("%d%d%d",&m,&n,&q);
120         init();
121         for(int i=1; i<=n; i++)
122         {
123             int tmp;
124             scanf("%d",&tmp);
125             isRED[tmp]=1;
126         }
127         for(int i=1; i<m; i++)
128         {
129             int a,b,c;
130             scanf("%d%d%d",&a,&b,&c);
131             add(a,b,c);
132             add(b,a,c);
133         }
134         dis[1]=0;
135         dfs(1,0,1);
136         ST.init(tot);
137         while(q--)
138         {
139             int N;
140             scanf("%d",&N);
141             for(int i=1; i<=N; i++)scanf("%d",&subnum[i]);
142             sort(subnum+1,subnum+1+N,cmp);
143             ll l=0,r=DIS[subnum[1]];
144             while(l < r)
145             {
146                 ll mid = (l+r)/2;
147                 if(check(mid,N))
148                 {
149                     r=mid;
150                 }
151                 else l=mid+1;
152             }
153             printf("%lld\n",r);
154         }
155     }
156 }