关于Noise and Error主题的一些小知识

（一）Noise会不会对VC bound产生影响？

此笔记源于台湾大学林轩田老师《机器学习基石》《机器学习技法》

 

答案是不会。

当信号中加入了Noise，其实对我们之前学过的内容不产生任何本质上的影响。

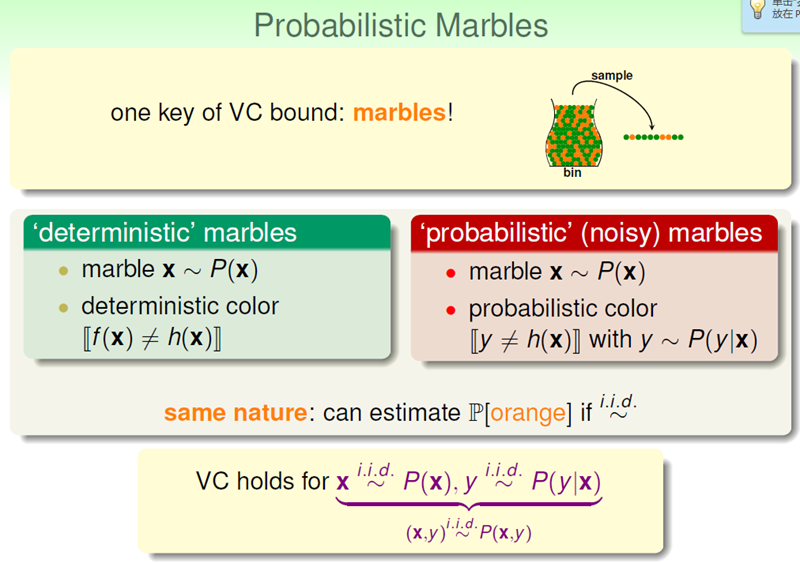
之前《机器学习真的起作用吗？》中的分析是基于：training dataset D的来源是：（x，f(x)）。其中x从服从某一概率分布P。

现在noise对数据产生了什么影响？之前，f(x)是确定的。现在f(x)不确定了。因为Noise的存在会影响f(x)的值。此时y更像是服从某一概率分布。但是抽样的一瞬间，y是确定的值。我们要估计的就是抽样这一瞬间，整体中的x和y。

如上，根本不影响我们的理论分析。

 

                                                        （二）err与err’

根据之前我们的学习，我们知道，Learning Algorithm A的一个重要的原则是：使得E_in很小（即选择的g在inside D上犯的错误很小）。

g在D上犯得错误记作err。

同时我们知道，错误的评估函数也是A的重要组成部分，记作err’。

理论上来说：err’=err.

但是在实际中很难实现，我们甚至无法准确地描述err是什么样子的。又或者err非常不利于计算。

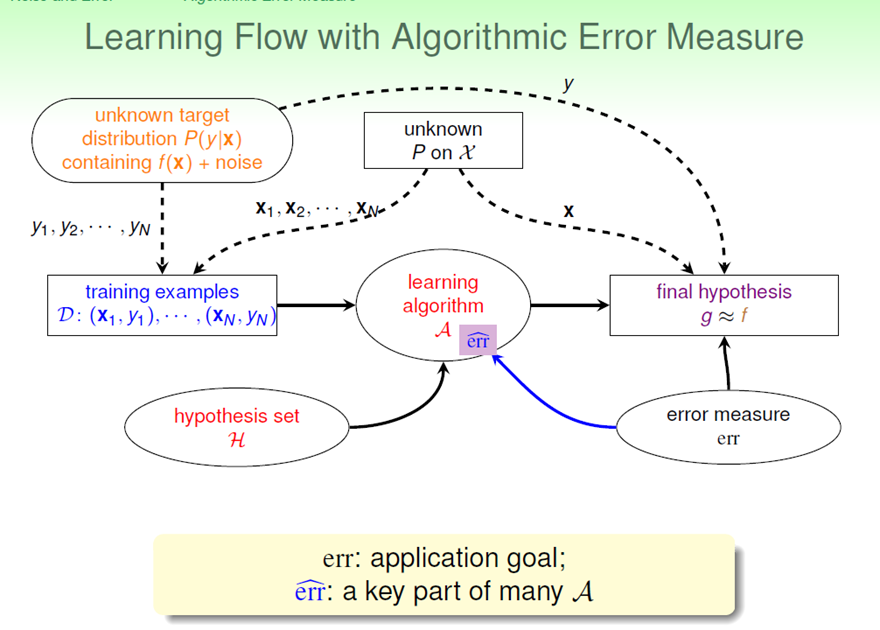
通常情况下，我们使用不同于err的err’作为A的key part。

上面这个流程图是一个机器学习的基本流程：其中我们使用err’进行学习，使用真正的err进行评估。

转载于:https://www.cnblogs.com/wangyanphp/p/5439021.html