高精度算法与数学函数计算-优快云博客

PASCAL版

//求阶乘
function fac(n:longint):longint;
var i:longint;
begin
    fac:=1;
    for i:=2 to n do fac:=fac*i;
end;

//素数判断
function prime(a:longint):boolean;
var i:longint;
begin
    if a<2 then exit(false);
    for i:=2 to trunc(sqrt(a)) do
        if a mod i=0 then exit(false);
    exit(true);
end;//最大公约、最小公倍
function GCD(a,b:longint):longint;
begin
    if b=0 then exit(a) else exit(GCD(b,a mod b));
end;
function LCM(a,b:longint):longint;
begin
    exit(a*b div GCD(a,b));
end;

//进制转换(<10) 
function conv(a,n:longint):string;
begin
    conv:='';
    while a>0 do
    begin
        conv:=chr((a mod n)+48)+conv;
        a:=a div n;
    end;
end;


//进制转换(>=10)
const
    r:array[0..19]of char=('0','1','2','3','4','5','6','7','8','9','A','B','C','D','E','F','G','H','I','J');
function conv(a,n:longint):string;
begin
    conv:='';
    while a>0 do
    begin
        conv:=r[a mod n]+conv;
        a:=a div n;
    end;
end;



//回文判断(字符串版)
function PLD(s:string):boolean;
var len,i:longint;
begin
    len:=length(s);
    for i:=1 to len div 2 do
        if s[i]<>s[len+1-i] then exit(false);
    exit(true);
end;




//回文判断(数值版)
function REV(a:longint):longint;
begin
    REV:=0;
    while a>0 do
    begin
        REV:=REV*10+a mod 10;
        a:=a div 10;
    end;
end;
function PLD(a:longint):boolean;
begin
    exit(a=REV(a));
end;

//快速排序(最终版)
procedure Qsort(l,r:longint);
var mid,i,j,t:longint;
begin
    i:=l; j:=r; mid:=a[(l+r) div 2];
    repeat
        while a[i]<mid do inc(i);
        while a[j]>mid do dec(j);
        if i<=j then
        begin
            t:=a[i]; a[i]:=a[j]; a[j]:=t;
            inc(i); dec(j);
        end;
    until i>j;
    if i<r then Qsort(i,r);
    if l<j then Qsort(l,j);
end;

var
    i,j,n:longint;
    prime:array[1..1000] of boolean;
begin
    prime[1]:=FALSE;
    for i:=1 to 1000 do prime[i]:=true;
    for i:=2 to trunc(sqrt(1000)) do
        if prime[i] then
            for j:=2 to 1000 div i do prime[i*j]:=false;
end.

高精算法模板(2的100次方求法)

const
    maxn=1000;
var
    n,i,j,k:longint;
    a:array[1..maxn] of longint;
begin
    a[1]:=1;
    for i:=1 to 100 do
    begin
        for j:=1 to maxn do a[j]:=a[j]*2;
        for j:=1 to maxn-1 do
        begin
            inc(a[j+1],a[j] div 10);
            a[j]:=a[j] mod 10;
        end;
    end;
    k:=maxn;
    while(a[k]=0) do dec(k);
    for i:=k downto 1 do write(a[i]);
    writeln;
end.

高精算法模板(2的100次方求法)

int gcd(int a,int b){return b?gcd(b,a%b):a;}
int lcm(int a,int b){return a/gcd(a,b)*b;}

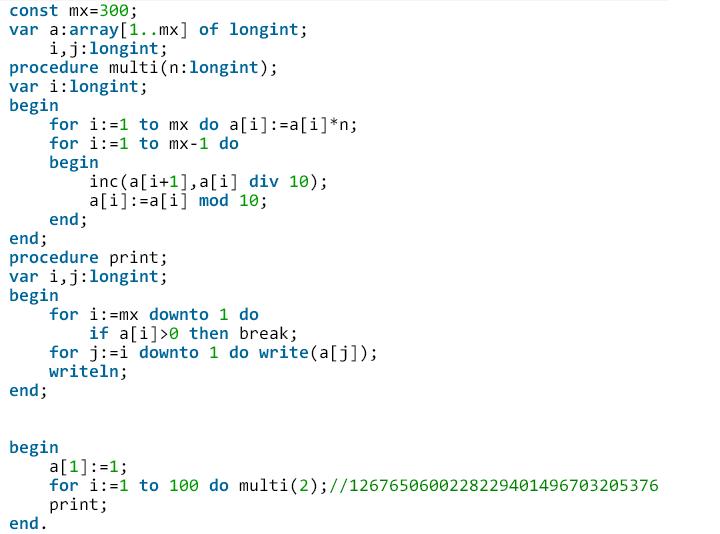
Catalan数高精版（n<=5000）

#include <stdio.h>
int a[5100][800],len;
void catalan(int n){ //求卡特兰数
    int i, j,  carry, temp;
    a[1][0] = 1;
    len = 1;
    for(i = 2; i <= n; i++){
        for(j = 0; j < len; j++) //乘法
        a[i][j] = a[i-1][j]*(4*(i-1)+2);
        carry = 0;
        for(j = 0; j < len; j++){ //处理相乘结果
            temp = a[i][j] + carry;
            a[i][j] = temp % 10000;
            carry = temp / 10000;
        }
        while(carry){ //进位处理
            a[i][len++] = carry % 10000;
            carry /= 10000;
        }
        carry = 0;
        for(j = len-1; j >= 0; j--){ //除法
            temp = carry*10000 + a[i][j];
            a[i][j] = temp/(i+1);
            carry = temp%(i+1);
        }
        while(!a[i][len-1])len--; //高位零处理
    }
}
int main(){
    int n,i;
    scanf("%d",&n);
    catalan(n);
    //printf("%d\n",len);
    printf("%d",a[n][len-1]);
    for(i=len-2;i>=0;i--)printf("%04d",a[n][i]);
    puts("");
    return 0;
}

//筛选法求素数（向Eratosthenes致敬）

var
    a:array[1..1000000] of boolean;
    p:array[1..150000] of longint;
    t,n:longint;
procedure Sieve(n:longint);
var i,j:longint;
begin
    for i:=2 to trunc(sqrt(n)) do
        if a[i] then
            for j:=2 to n div i do a[i*j]:=false;
    t:=0;
    for i:=2 to n do
        if a[i] then begin inc(t);p[t]:=i;end;  
end;

begin
    fillchar(a,sizeof(a),true);
    Sieve(1000000);
    writeln(t,' ',p[3]);//78498 5
end.

转载于:https://www.cnblogs.com/qilinart/articles/3237387.html